
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内单调递减,求
内单调递减,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(1)求导![]() ,对k分类讨论,得到函数的单调区间;(2)函数
,对k分类讨论,得到函数的单调区间;(2)函数![]() 在区间
在区间![]() 内单调递减,即不等式在
内单调递减,即不等式在![]() 在
在![]() 上成立,利用二次函数的图象与性质,易得
上成立,利用二次函数的图象与性质,易得![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.
![]() ,
,
(1)当![]() 时,令
时,令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递增函数;
为单调递增函数;
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递减函数.
为单调递减函数.
(2)当![]() 时,
时,
①当![]() ,即
,即![]() 时,
时,
令![]() ,解得
,解得![]() 或
或![]() ,此时函数
,此时函数![]() 为单调递增函数;
为单调递增函数;
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递减函数.
为单调递减函数.
②当![]() 时,
时, ![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
③当![]() ,即
,即![]() 时,
时,
令![]() ,解得
,解得![]() 或
或![]() ,此时函数
,此时函数![]() 为单调递增函数;
为单调递增函数;
令![]() ,解得
,解得![]() ,此时函数
,此时函数![]() 为单调递减函数.
为单调递减函数.
综上所述,
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
, ![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
, ![]() ,单调递减区间为
,单调递减区间为![]() .
.
(Ⅱ)![]() ,
,
因为函数![]() 在
在![]() 内单调递减,所以不等式在
内单调递减,所以不等式在![]() 在
在![]() 上成立.
上成立.
设![]() ,则
,则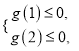 即
即![]() 解得
解得![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的a,b∈R,都有f(a+b)=f(a)+f(b)﹣1,且当x>0时,f(x)>1
(1)判断并证明f(x)的单调性;
(2)若f(4)=3,解不等式f(3m2﹣m﹣2)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:kx﹣y+1+2k=0(k∈R) (Ⅰ)证明直线l经过定点并求此点的坐标;
(Ⅱ)若直线l不经过第四象限,求k的取值范围;
(Ⅲ)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 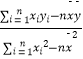 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4—4:坐标系与参数方程】
将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线![]() 与C的交点为
与C的交点为![]() ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三内角A、B、C的对边分别是a、b、c,且b(sinB﹣sinC)+(c﹣a)(sinA+sinC)=0 (Ⅰ)求角A的大小;
(Ⅱ)若a= ![]() ,sinC=
,sinC= ![]() sinB,求△ABC的面积.
sinB,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com