
分析 (1)令x=1,则${a_0}={3^n}$,再令x=2,则$\sum_{i=0}^n{a_i}={4^n}$,可得Sn=$\sum_{i=1}^{n}$ai 的值.
(2)要比较Sn与(n-2)3n+2n2的大小,只要比较4n与(n-1)3n+2n2的大小.检验可得当n=1或4或5时,4n>(n-1)3n+2n2,当n=2或3或4时,4n>(n-1)3n+2n2.猜测当n≥5时,4n>(n-1)3n+2n2,再用数学归纳法、放缩法证明结论.
解答 解:(1)令x=1,则${a_0}={3^n}$,令x=2,则$\sum_{i=0}^n{a_i}={4^n}$,所以Sn=$\sum_{i=1}^{n}$ai =4n-3n.
(2)要比较Sn与(n-2)3n+2n2的大小,只要比较4n与(n-1)3n+2n2的大小.
当n=1时,4n>(n-1)3n+2n2,当n=2或3时,4n<(n-1)3n+2n2,
当n=4时,4n<(n-1)3n+2n2 ,
当n=5时,4n>(n-1)3n+2n2.
猜想:当n≥5时,4n>(n-1)3n+2n2.下面用数学归纳法证明:
①由上述过程可知,当n=5时,结论成立.
②假设当n=k(k≥4,k∈N*)时结论成立,即4k>(k-1)3k+2k2,
两边同乘以4,得4k+1>4[(k-1)3k+2k2]=k3k+1+2(k+1)2+[(k-4)3k+6k2-4k-2],
而(k-4)3k+6k2-4k-2=(k-4)3k+6(k2-k-2)+2k+10=(k-4)3k+6(k-2)(k+1)+2k+10>0,
所以4k+1>[(k+1)-1]3k+1+2(k+1)2,
即n=k+1时结论也成立.
由①②可知,当n≥4时,4n>(n-1)3n+2n2成立.
综上所述,当n=1时,${S_n}>(n-2){3^n}+2{n^2}$;当n=2或3时,4n<(n-1)3n+2n2,Sn<(n-2)3n+2n2;
当n≥5时,${S_n}>(n-2){3^n}+2{n^2}$.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,用数学归纳法、放缩法证明不等式,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 9 | D. | -9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.
已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
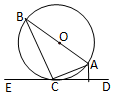 如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )
如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是( )| A. | 4π | B. | 6π | C. | 8π | D. | 16π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com