
【题目】设函数f(x)=|x+m|.
(Ⅰ) 解关于m的不等式f(1)+f(﹣2)≥5;
(Ⅱ)当x≠0时,证明: ![]() .
.
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 
(1)求证:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,某地最近几年某商品的需求量逐年上升.下表为部分统计数据:
年份 |
|
|
|
|
|
需求量 |
|
|
|
|
|
为了研究计算的方便,工作人员将上表的数据进行了处理,令![]() ,
,![]() .
.
(1)填写下列表格并求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
时间代号 | |||||
|
(2)根据所求的线性回归方程,预测到![]() 年年底,某地对该商品的需求量是多少?
年年底,某地对该商品的需求量是多少?
(附:线性回归方程![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】O为坐标原点,直线l与圆x2+y2=2相切.
(1)若直线l分别与x、y轴正半轴交于A、B两点,求△AOB面积的最小值及面积取得最小值时的直线l的方程.
(2)设直线l交椭圆 ![]() =1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
=1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E. 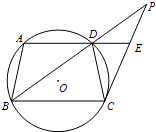
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解当下高二男生的身高状况,某地区对高二年级男生的身高(单位: ![]() )进行了抽样调查,得到的频率分布直方图如图所示.已知身高在
)进行了抽样调查,得到的频率分布直方图如图所示.已知身高在![]() 之间的男生人数比身高在
之间的男生人数比身高在![]() 之间的人数少1人.
之间的人数少1人.

(1)若身高在![]() 以内的定义为身高正常,而该地区共有高二男生18000人,则该地区高二男生中身高正常的大约有多少人?
以内的定义为身高正常,而该地区共有高二男生18000人,则该地区高二男生中身高正常的大约有多少人?
(2)从所抽取的样本中身高在![]() 和
和![]() 的男生中随机再选出2人调查其平时体育锻炼习惯对身高的影响,则所选出的2人中至少有一人身高大于185
的男生中随机再选出2人调查其平时体育锻炼习惯对身高的影响,则所选出的2人中至少有一人身高大于185![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为创建“绿色校园”,在校园内种植树木,有A、B、C三种树木可供选择,已知这三种树木6年内的生长规律如下:
A树木:种植前树木高0.84米,第一年能长高0.1米,以后每年比上一年多长高0.2米;
B树木:种植前树木高0.84米,第一年能长高0.04米,以后每年生长的高度是上一年生长高度的2倍;
C树木:树木的高度![]() (单位:米)与生长年限
(单位:米)与生长年限![]() (单位:年,
(单位:年,![]() )满足如下函数:
)满足如下函数:![]() (
(![]() 表示种植前树木的高度,取
表示种植前树木的高度,取![]() ).
).
(1)若要求6年内树木的高度超过5米,你会选择哪种树木?为什么?
(2)若选C树木,从种植起的6年内,第几年内生长最快?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各![]() 种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(Ⅰ)如果抢到红包个数超过![]() 个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有
个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有![]() 的把握认为抢到红包的个数与手机品牌有关?
的把握认为抢到红包的个数与手机品牌有关?
(Ⅱ)不考虑其它因素,现要从甲、乙两品牌的![]() 种型号中各选出
种型号中各选出![]() 种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
参考公式:随机变量![]() 的观察值计算公式:
的观察值计算公式:![]() ,
,
其中![]() .临界值表:
.临界值表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com