
【题目】已知非空集合![]() 是由一些函数组成,满足如下性质:①对任意
是由一些函数组成,满足如下性质:①对任意![]() ,
,![]() 均存在反函数
均存在反函数![]() ,且
,且![]() ;②对任意
;②对任意![]() ,方程
,方程![]() 均有解;③对任意
均有解;③对任意![]() 、
、![]() ,若函数
,若函数![]() 为定义在
为定义在![]() 上的一次函数,则
上的一次函数,则![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求证:函数
中,求证:函数![]() ;
;
(2)若函数![]() (
(![]() )在集合
)在集合![]() 中,求实数
中,求实数![]() 的取值范围;
的取值范围;
(3)若集合![]() 中的函数均为定义在
中的函数均为定义在![]() 上的一次函数,求证:存在一个实数
上的一次函数,求证:存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.
【答案】(1)见详解;(2)![]() ;(3)见详解;
;(3)见详解;
【解析】
(1)由![]() ,根据性质①可得
,根据性质①可得![]() ,且存在
,且存在![]() ,使得
,使得
![]() ,由
,由![]() ,且为一次函数,根据性质③即可证明.
,且为一次函数,根据性质③即可证明.
(2)由性质②,方程![]() ,即
,即![]() 在
在![]() 上有解,可得
上有解,可得![]() ,
,
变形![]() ,
,![]() .对
.对![]() 与
与![]() 的关系分类讨论,利用基本不等式的性质即可求解.
的关系分类讨论,利用基本不等式的性质即可求解.
(3)任取![]() ,
,![]() ,由性质①
,由性质①![]() ,不妨设
,不妨设![]() ,
,
(若![]() ,则
,则![]() ,
,![]() ),
),
由性质③函数![]() ,
,
由性质①:![]() ,
,
由性质③:![]()
由性质②方程:![]() ,可得
,可得![]() ,即
,即![]() ,即可得证.
,即可得证.
(1)由![]() ,根据性质①可得
,根据性质①可得![]() ,且存在
,且存在![]() ,使得
,使得
![]() ,由
,由![]() ,且为一次函数,
,且为一次函数,
根据性质③可得:![]() .
.
(2)由性质②,方程![]() ,即
,即![]() 在
在![]() 上有解,
上有解,![]() ,
,
由![]()
![]() ,
,
若![]() ,
,![]() 时,
时,![]() ,且
,且![]() ,
,
![]() 此时
此时![]() 没有反函数,即不满足性质①.
没有反函数,即不满足性质①.
若![]() ,
,![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 此时
此时![]() 有反函数,
有反函数,
即满足性质①.
综上:![]() .
.
(3)任取![]() ,
,![]() ,由性质①
,由性质①![]() ,不妨设
,不妨设![]() ,
,
(若![]() ,则
,则![]() ,
,![]() ),
),
由性质③函数![]() ,
,
由性质①:![]() ,
,
由性质③:![]()
由性质②方程:![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() ,可得
,可得![]() ,
,![]() ,
,
![]() ,可得
,可得![]() ,
,![]() ,
,
由此可知:对于任意两个函数![]() ,
,![]() ,
,
存在相同的![]() 满足:
满足:![]() ,
,
![]() 存在一个实数
存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案科目:高中数学 来源: 题型:
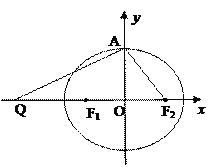
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
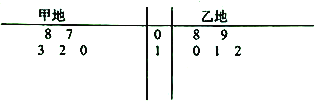
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
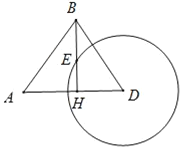
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其北偏东
处,此时测得其北偏东![]() 方向与它相距
方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.
(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方航行.为了将该船拦截在离
海里的速度沿正南方航行.为了将该船拦截在离![]() 岛
岛![]() 海里的
海里的![]() 处(
处(![]() 在
在![]() 的正南方向),不让其进入
的正南方向),不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值(角度精确到
海里内的海域,试确定海监船的航向,并求其速度的最小值(角度精确到![]() ,速度精确到
,速度精确到![]() 海里/小时).
海里/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() 是定义在
是定义在![]() 上的单调函数,求实数a的取值范围;
上的单调函数,求实数a的取值范围;
(2)当![]() 时,判断
时,判断![]() 与
与![]() 的图象在其公共点处是否存在公切线?若存在,求满足条件的a值的个数;若不存在,请说明理由.
的图象在其公共点处是否存在公切线?若存在,求满足条件的a值的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,四边形
,四边形![]() 与四边形
与四边形![]() 也都为正方形,连接
也都为正方形,连接![]() ,点
,点![]() 为
为![]() 的中点,有下述四个结论:
的中点,有下述四个结论:
①![]() ; ②
; ②![]() 与
与![]() 所成角为
所成角为![]() ;
;
③![]() 平面
平面![]() ; ④
; ④![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西湖小学为了丰富学生的课余生活开设课后少年宫活动,其中面向二年级的学生共开设了三门课外活动课:七巧板、健美操、剪纸.203班有包括奔奔、果果在内的5位同学报名参加了少年宫活动,每位同学只能挑选一门课外活动课,已知每门课都有人选,则奔奔和果果选择了同一个课外活动课的选课方法种数为( )
A.18B.36C.72D.144
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com