
【题目】(本题满分14分)如图,我市有一个健身公园,由一个直径为2km的半圆和一个以![]() 为斜边的等腰直角三角形
为斜边的等腰直角三角形![]() 构成,其中
构成,其中![]() 为
为![]() 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道![]() ,按实际需要,四边形
,按实际需要,四边形![]() 的两个顶点
的两个顶点![]() 分别在线段
分别在线段![]() 上,另外两个顶点
上,另外两个顶点![]() 在半圆上,
在半圆上, ![]() ,且
,且![]() 间的距离为1km.设四边形
间的距离为1km.设四边形![]() 的周长为
的周长为![]() km.
km.

(1)若![]() 分别为
分别为![]() 的中点,求
的中点,求![]() 长;
长;
(2)求周长![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)求![]() 长,就是求圆中弦长,关键求出圆心到弦所在直线距离:因为
长,就是求圆中弦长,关键求出圆心到弦所在直线距离:因为![]() 分别为
分别为![]() 的中点,所以圆心到直线CD距离为半径的一半,即
的中点,所以圆心到直线CD距离为半径的一半,即![]() ,又
,又![]() 间的距离为1km,所以圆心到弦所在直线距离为
间的距离为1km,所以圆心到弦所在直线距离为![]() ,因此
,因此![]()
(2)求四边形![]() 的周长,就是要表示出四边长度,如何取自变量是解决问题的关键,设角是一个较好的方法,如设
的周长,就是要表示出四边长度,如何取自变量是解决问题的关键,设角是一个较好的方法,如设![]() ,其中M为AB中点,则
,其中M为AB中点,则![]() ,
,![]() ,
,![]() ,再根据基本不等式其周长最值
,再根据基本不等式其周长最值
试题解析:(1)解:连结![]() 并延长分别交
并延长分别交![]() 于
于![]() ,连结
,连结![]() ,
,
∵![]() 分别为
分别为![]() 的中点,
的中点,![]() ,∴
,∴![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为斜边,
为斜边,![]() ,
,
![]() .∵
.∵![]() ,∴
,∴![]() . 3分
. 3分
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴![]() . 6分
. 6分
(2)解法1 设![]() ,
,![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() , 8分
, 8分
∴![]() 10分
10分
![]() ,(当
,(当![]() 或
或![]() 时取等号)
时取等号)
∴当![]() 或
或![]() 时,周长
时,周长![]() 的最大值为
的最大值为![]()
![]() . 14分
. 14分
解法2 以![]() 为原点,
为原点,![]() 为
为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() . 8分
. 8分
∴![]() 10分
10分
![]() ,
,
(当![]() ,
,![]() 或
或![]() ,
,![]() 时取等号)
时取等号)
∴当![]() ,
,![]() 或
或![]() ,
,![]() 时,周长
时,周长![]() 的最大值为
的最大值为![]()
![]() . 14分
. 14分


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】如图(a),在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=8,AD=CD=4,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D﹣ABC,如图(b)所示. 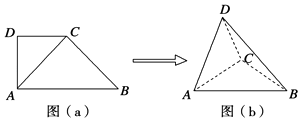
(1)求证:BC⊥平面ACD;
(2)求几何体D﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为 .
(注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …,xn的平均数)
为x1 , x2 , …,xn的平均数)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 在线段
在线段![]() 上(点
上(点![]() 与点
与点![]() 不重合).
不重合).

(1)若异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ,求
,求![]() 的长度;
的长度;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,D,E分别是BC,AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P﹣BC﹣A的平面角为γ,则α,β,γ的大小关系是( ) 
A.α<β<γ
B.α<γ<β
C.β<α<γ
D.γ<β<α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x0 , x0+ ![]() 是函数f(x)=cos2(wx﹣
是函数f(x)=cos2(wx﹣ ![]() )﹣sin2wx(ω>0)的两个相邻的零点
)﹣sin2wx(ω>0)的两个相邻的零点
(1)求 ![]() 的值;
的值;
(2)若对 ![]() ,都有|f(x)﹣m|≤1,求实数m的取值范围.
,都有|f(x)﹣m|≤1,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
已知抛物线![]() 的焦点为
的焦点为![]() ,
, ![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为
的横坐标为![]() 时,
时, ![]() 为正三角形.
为正三角形.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和
和![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,
(ⅰ)证明直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(ⅱ)![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com