分析:(1)先证明A
1C⊥EF.建立空间直角坐标系,则可求得如下点的坐标:A
1,C,E,设点P的坐标为(1,m,0),则通过
•=0,求出m=1-λ,即可求出
的值.
(2)由(1)知说明A
1C⊥平面AB
1D
1且过△AB
1D
1的中心,A
1C⊥平面C
1BD且过△C
1BD的中心.正方体在平面EFP内的射影相当于正方体在平面C
1BD内的射影,求出BD,求出正六边形边长,求出射影面积.
解答:解:(1)∵
=λ,=λ,∴EF∥B
1D
1,A
1C在平面A
1B
1C
1D
1上的射影为A
1C
1,
∵A
1C
1⊥B
1D
1,∴A
1C⊥B
1D
1,∴A
1C⊥EF.如图建立空间直角坐
标系,则可求得如下点的坐标:A
1(1,0,1),C(0,1,0),E(0,1-λ,1),
设点P的坐标为(1,m,0),则
=(-1,1,-1,),=(-1,1-λ-m,1),若A
1C⊥EP,则有
•=(-1,1,-1,)•(-1,1-λ-m,1)=1-λ-m=0,
∴m=1-λ,即
的值为1-λ.
(2)由(1)知A
1C⊥B
1D
1,同理A
1C⊥AB
1,即A
1C⊥平面AB
1D
1且过△AB
1D
1的中心,同理即A
1C⊥平面C
1BD且过△C
1BD的中心.于是正方体在平面EFP内的射影相当于正方体在平面C
1BD内的射影,而正三角形AB
1D
1中心P在平面C
1BD内的射影是正三角形C
1BD的中心Q,于是AB
1D
1在平面C
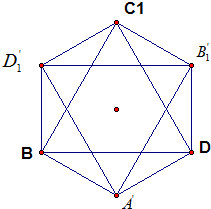
1BD内的射影如图所示,
于是正六边形
BA′DC1即为正方体在平面C
1BD的射影,BD=
,
故正六边形边长为
=,故射影面积为
6××()2=.
点评:本题考查直线与平面垂直判定定理的应用,利用空间直角坐标系向量法说明垂直的应用,射影面积的求法,考查空间想象能力与计算能力.




 名校课堂系列答案
名校课堂系列答案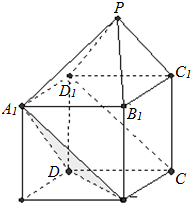 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=