
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知过点![]() 的圆
的圆![]() 和直线
和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() ,圆
,圆![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() 若存在,求出点
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表:
周数x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散点图:

(2)根据上表数据用最小二乘法求出y关于x的线性回归方程 (精确到0.01);
(3)根据经验,观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及其以上为重度焦虑,若为中度焦虑及其以上,则要进行心理疏导,若一个学生在距高考第二周时观测值为100,则该学生是否需要进行心理疏导?
(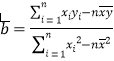 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分15分)
在等差数列{an}中,a1=1,公差d≠0,且a1,a2,a5是等比数列{bn}的前三项.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=an·bn,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个生产公司投资A生产线500万元,每万元可创造利润![]() 万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了
万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了![]() ;若将少用的x万元全部投入B生产线,每万元创造的利润为
;若将少用的x万元全部投入B生产线,每万元创造的利润为![]() 万元,其中
万元,其中![]() .
.
![]() 若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
![]() 若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国校足办决定于2019年8月组织开展全国青少年校园足球夏令营总营活动.某校购买![]() 两种不同品牌的足球,其中
两种不同品牌的足球,其中![]() 种品牌足球
种品牌足球![]() 个,
个,![]() 种品牌足球
种品牌足球![]() 个,共需元
个,共需元![]() ,已知
,已知![]() 种品牌足球的售价比
种品牌足球的售价比![]() 种品牌足球的售价高
种品牌足球的售价高![]() 元/个.
元/个.
(1)求![]() 两种品牌足球的售价;
两种品牌足球的售价;
(2)该校为举办足球联谊赛,决定第二次购买![]() 两种不同品牌的足球.恰逄商场对两种品牌足球的售价进行调整,
两种不同品牌的足球.恰逄商场对两种品牌足球的售价进行调整,![]() 种品牌足球售价比第一次购买时提高了
种品牌足球售价比第一次购买时提高了![]() 元/个
元/个![]() ,
,![]() 种品牌足球按第一次购买时售价的
种品牌足球按第一次购买时售价的![]() 折(即原价的
折(即原价的![]() )出售.如果第二次购买
)出售.如果第二次购买![]() 种品牌足球的个数比第一次少
种品牌足球的个数比第一次少![]() 个,第二次购买
个,第二次购买![]() 种品牌足球的个数比第一次多
种品牌足球的个数比第一次多![]() 个,则第二次购买
个,则第二次购买![]() 两种品牌足球的总费用比第一次少
两种品牌足球的总费用比第一次少![]() 元.求
元.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[e,+∞)上的函数f(x)满足f(x)+xlnxf′(x)<0且f(2018)=0,其中f′(x)是函数![]() 的导函数,e是自然对数的底数,则不等式f(x)>0的解集为( )
的导函数,e是自然对数的底数,则不等式f(x)>0的解集为( )
A. [e,2018) B. [2018,+∞) C. (e,+∞) D. [e,e+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com