
如图,平面EAD⊥平面ABCD,△ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点,EC与平面ABCD成 角.
角.

(Ⅰ)求证:EG⊥平面ABCD;
(Ⅱ)若AD=2,求二面角E-FC-G的度数;
(Ⅲ)当AD的长是多少时,D点到平面EFC的距离为2?请说明理由.
|
证明:(Ⅰ)∵△ADE是正三角形,∴EG⊥AD. 又平面ADE⊥平面ABCD且相交于AD,∴EG⊥平面ABCD. 解:(Ⅱ)连接CG,则CG是EC在平面ABCD内的射影. ∴∠ECG是EC与平面ABCD所成的角,即∠ECG= 在Rt△EGC中:∵AD=2,∴EG= 在Rt△GDC中:DG=1,GC=3,∴DC= 则 ∴ ∵GF是EF在平面AC内的射影,∴EF⊥FC, ∴∠EFG是二面角E-FC-G的平面角. 在Rt△EGF中,EG=GF= 故所求二面角E-FC-D的度数为 (Ⅲ)连DF,D到平面EFC的距离即为三棱锥D-EFC的高. ∵ 设AD=a,则CD= 故AD的长为 |


科目:高中数学 来源: 题型:
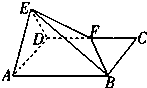 如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角.
如图,平面EAD⊥平面ABCD,△EAD为正三角形,四边形ABCD为矩形,F是CD中点,EB与平面ABCD成30°角.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
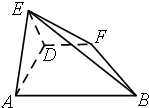 如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=
如图,平面EAD⊥平面ABFD,△AED为正三角形,四边形ABFD为直角梯形,且∠BAD=90°,AB∥DF,AD=a,AB=| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年内蒙古赤峰市高三统考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com