
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 数列![]() 的前
的前![]() 项和为
项和为![]() B. 数列
B. 数列![]() 的通项公式为
的通项公式为![]()
C. 数列![]() 为递增数列 D. 数列
为递增数列 D. 数列![]() 是递增数列
是递增数列
【答案】C
【解析】
方法一:根据数列的递推公式可得{![]() }是以5为首项,以5为等差的等差数列,可得Sn=
}是以5为首项,以5为等差的等差数列,可得Sn=![]() ,an=
,an=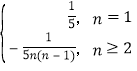 ,即可判断,
,即可判断,
方法二:当n=1时,分别代入A,B,可得A,B错误,当n=2时,a2+5a1(a1+a2)=0,即a2+![]() +a2=0,可得a2=﹣
+a2=0,可得a2=﹣![]() ,故D错误,
,故D错误,
方法一:∵an+5Sn﹣1Sn=0,
∴Sn﹣Sn﹣1+5Sn﹣1Sn=0,
∵Sn≠0,
∴![]() ﹣
﹣![]() =5,
=5,
∵a1=![]() ,
,
∴![]() =5,
=5,
∴{![]() }是以5为首项,以5为等差的等差数列,
}是以5为首项,以5为等差的等差数列,
∴![]() =5+5(n﹣1)=5n,
=5+5(n﹣1)=5n,
∴Sn=![]() ,
,
当n=1时,a1=![]() ,
,
当n≥2时,
∴an=Sn﹣Sn﹣1=![]() ﹣
﹣![]() =
=![]() ,
,
∴an=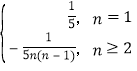 ,
,
故只有C正确,
方法二:当n=1时,分别代入A,B,可得A,B错误,
当n=2时,a2+5a1(a1+a2)=0,即a2+![]() +a2=0,可得a2=﹣
+a2=0,可得a2=﹣![]() ,故D错误,
,故D错误,
故选:C.


科目:高中数学 来源: 题型:
【题目】数列{![]() }的前
}的前![]() 项和为Sn,且Sn=n(n+1)(n∈N*).
项和为Sn,且Sn=n(n+1)(n∈N*).
(1)若数列![]() 满足:
满足:![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列{
,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
(3)![]()
![]() ,(n为正整数),问是否存在非零整数
,(n为正整数),问是否存在非零整数![]() ,使得对任意正整数n,都有
,使得对任意正整数n,都有![]() 若存在,求
若存在,求![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在样本的频率分布直方图中共有![]() 个小矩形,若中间一个小矩形的面积等于其余
个小矩形,若中间一个小矩形的面积等于其余![]() 个小矩形面积的
个小矩形面积的![]() ,且样本容量为3200,则中间一组的频数为__________.
,且样本容量为3200,则中间一组的频数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
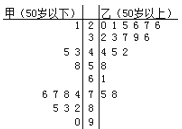
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了 30 名同学,得到如下的 ![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用学习成绩优秀的 12 名同学中,随机抽取 2 名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中倍抽取的 5 名同学,再随机抽取 3 名同学,试求抽取 3 名同学中恰有 2 名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com