
已知函数
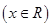 满足
满足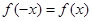 ,
,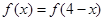 ,且当
,且当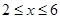 时,
时,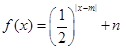 .
.
(1)证明:函数 是周期函数;(2)若
是周期函数;(2)若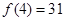 ,求
,求 的值.
的值.
科目:高中数学 来源: 题型:解答题
如图所示,某人想制造一个支架,它由四根金属杆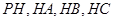 构成,其底端三点
构成,其底端三点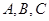 均匀地固定在半径为
均匀地固定在半径为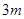 的圆
的圆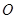 上(圆
上(圆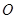 在地面上),
在地面上),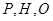 三点相异且共线,
三点相异且共线,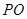 与地面垂直. 现要求点
与地面垂直. 现要求点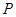 到地面的距离恰为
到地面的距离恰为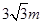 ,记用料总长为
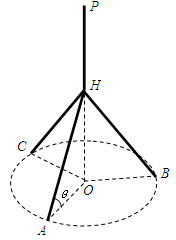
,记用料总长为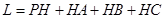 ,设
,设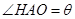 .
.
(1)试将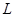 表示为
表示为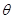 的函数,并注明定义域;
的函数,并注明定义域;
(2)当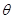 的正弦值是多少时,用料最省?
的正弦值是多少时,用料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x+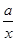 (x≠0,a∈R).
(x≠0,a∈R).
(1)当a=4时,证明:函数f(x)在区间[2,+∞)上单调递增;
(2)若函数f(x)在[2,+∞)上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若f (x)是定义在R上的偶函数,其图象关于直线x=2对称,且当x∈(-2, 2) 时,f (x) =-x2+1. 则当x∈(-6,-2)时,f(x)=_______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com