
 .
.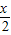 ,剩下的式子利用平方差公式及二倍角的余弦函数公式化简;分母被开方数提取2后,利用二倍角的余弦函数公式化简,再根据
,剩下的式子利用平方差公式及二倍角的余弦函数公式化简;分母被开方数提取2后,利用二倍角的余弦函数公式化简,再根据 =|a|进行变形,由x的范围求出
=|a|进行变形,由x的范围求出 的范围,根据绝对值的代数意义进行化简,最后分子分母约分后即可最简的函数f(x)的解析式;
的范围,根据绝对值的代数意义进行化简,最后分子分母约分后即可最简的函数f(x)的解析式; =
=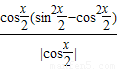 ,(4分)
,(4分)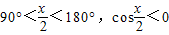 ,(5分)
,(5分) ;(6分)
;(6分) 的范围,进而化简绝对值,熟练掌握公式是第一问化简函数解析式的关键.
的范围,进而化简绝对值,熟练掌握公式是第一问化简函数解析式的关键. 

科目:高中数学 来源:2011-2012年学广东省梅州市东山中学高三(上)期中数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012年北京市海淀区高考数学二模试卷(理科)(解析版) 题型:解答题
 .
. 时,记函数f(x)的零点为x,若对任意x1,x2∈[0,x]且x2-x1=1,都有|f(x2)-f(x1)|≥m成立,求实数m的最大值.
时,记函数f(x)的零点为x,若对任意x1,x2∈[0,x]且x2-x1=1,都有|f(x2)-f(x1)|≥m成立,求实数m的最大值. ,
,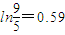 )
)查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省四校高三第一次联考数学试卷(理科)(解析版) 题型:解答题
 .
. 时,记函数f(x)的零点为x,若对任意x1,x2∈[0,x]且x2-x1=1,都有|f(x2)-f(x1)|≥m成立,求实数m的最大值.
时,记函数f(x)的零点为x,若对任意x1,x2∈[0,x]且x2-x1=1,都有|f(x2)-f(x1)|≥m成立,求实数m的最大值.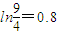 ,
, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com