
【题目】已知命题p:函数f(x)=(m2﹣1) ![]() 上为增函数;命题q:函数g(x)=x2﹣2elnx﹣m有零点.
上为增函数;命题q:函数g(x)=x2﹣2elnx﹣m有零点.
(I)若p∨q为假命题,求实数m的取值范围;
(Ⅱ)若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
【答案】解:若命题p为真命题,
即函数f(x)=(m2﹣1) ![]() 上为增函数,
上为增函数,
则m2﹣1>0,解得:m<﹣1,或m>1,
∵函数g(x)=x2﹣2elnx﹣m
∴g′(x)=2x﹣ ![]()
当x∈(0, ![]() )时,g′(x)<0,当x∈(
)时,g′(x)<0,当x∈( ![]() ,+∞)时,g′(x)>0,
,+∞)时,g′(x)>0,
故当x= ![]() 时,函数g(x)取最小值﹣m,
时,函数g(x)取最小值﹣m,
若命题q为真命题:函数g(x)=x2﹣2elnx﹣m有零点.
则:﹣m≤0,即m≥0,
(I)若p∨q为假命题,则p,q均为假命题,
则 ![]() ,
,
解得:﹣1≤m<0;
(Ⅱ)若p∨q为真命题,p∧q为假命题,则p,q一真一假,
若p真q假,则 ![]() ,解得:m<﹣1
,解得:m<﹣1
若p假q真,则 ![]() ,解得:0≤m≤1,
,解得:0≤m≤1,
综上可得:0≤m≤1,或m<﹣1
【解析】当命题p为真命题时,列出不等式,求出m的取值范围;利用导数讨论函数g(x)的单调性,求出函数g(x)的最小值,当命题q为真命题时写出m的取值范围;(1)若p![]() q为假命题,则p、q均为假命题;(2)若p
q为假命题,则p、q均为假命题;(2)若p![]() q为真命题,p
q为真命题,p![]() q为假命题,则p,q一真一假.
q为假命题,则p,q一真一假.
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】已知随圆E: ![]() +
+ ![]() =1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4
=1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4 ![]() ,则椭圆E的焦距的取值范围是( )
,则椭圆E的焦距的取值范围是( )
A.[2,+∞)
B.[4,+∞)
C.[2 ![]() ,+∞)
,+∞)
D.[4 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市2016年12个月的PM2.5平均浓度指数如图所示.由图判断,四个季度中PM2.5的平均浓度指数方差最小的是( ) 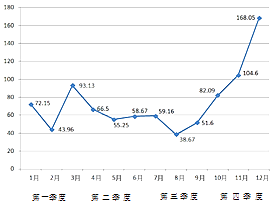
A.第一季度
B.第二季度
C.第三季度
D.第四季度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cos2x),
=(sinx,cos2x), ![]() =(
=( ![]() cosx,1),x∈R,设f(x)=
cosx,1),x∈R,设f(x)= ![]()
![]() .
.
(1)求f(x)的解析式及单调递增区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2,f(A)=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a,b,c,下列命题正确的是( )
A.若a>b,则ac2>bc2
B.若a<b<0,则a2>ab>b2
C.若a<b<0,则 ![]()
D.若a<b<0,则 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C的对边分别为a,b,c,已知A≠ ![]() ,且3sinAcosB+
,且3sinAcosB+ ![]() bsin2A=3sinC.
bsin2A=3sinC.
(I)求a的值;
(Ⅱ)若A= ![]() ,求△ABC周长的最大值.
,求△ABC周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax﹣x. (Ⅰ)若曲线y=f(x)在(0,f(0))处的切线l与直线x+2y+3=0垂直,求a的值;
(Ⅱ)当a≠1时,求证:存在实数x0使f(x0)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“x0∈R,x02﹣x0≤0”的否定是“x∈R,x2﹣x≥0”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com