
 =
= ,求
,求 的值;
的值;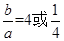 ;(2)
;(2) 最小值为4,此时
最小值为4,此时 为29;(3)详见解析
为29;(3)详见解析 ,等比数列的公比为
,等比数列的公比为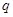 ,则
,则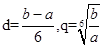 ,表示出
,表示出 ,又由
,又由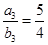 ,可得到
,可得到 ,解得
,解得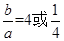 ;(2)由条件得
;(2)由条件得 ,即
,即 ,从而得
,从而得 ,又由于
,又由于 ,即
,即 ,从而得
,从而得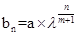 ,又题中有
,又题中有 ,可得
,可得 , 化简消去a得:
, 化简消去a得: ,观察此式结构特征:
,观察此式结构特征: ,则要求
,则要求 为有理数.即
为有理数.即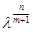 必须为有理数,而
必须为有理数,而 ,可将
,可将 用数字代入检验: 若
用数字代入检验: 若 ,则
,则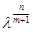 为无理数,不满足条件; 同理,
为无理数,不满足条件; 同理,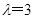 不满足条件; 当
不满足条件; 当 时,
时, .要使
.要使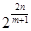 为有理数,则
为有理数,则 必须为整数,要满足
必须为整数,要满足  ,可解得
,可解得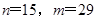 ;(3)可假设
;(3)可假设 ,
, 为数列
为数列 的前
的前 项的和,我们易先证:若
项的和,我们易先证:若 为递增数列,则
为递增数列,则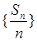 为递增数列;同理可证,若
为递增数列;同理可证,若 为递减数列,则
为递减数列,则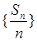 为递减数列;由于a和b的大小关系不确定,故要对其分类讨论:①当
为递减数列;由于a和b的大小关系不确定,故要对其分类讨论:①当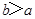 时,
时, .当
.当 时,
时,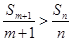 .即
.即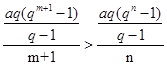 ,即
,即 .因为
.因为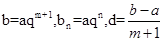 ,所以
,所以 ,即
,即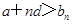 ,即
,即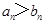 ;②当
;②当 时,同理可求得
时,同理可求得 .
. ,等比数列的公比为
,等比数列的公比为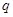 ,
,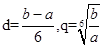 .
. . 2分
. 2分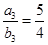 ,所以
,所以 ,解得
,解得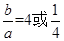 . 4分
. 4分 ,所以
,所以 ,从而得
,从而得 .
. ,所以
,所以 ,从而得
,从而得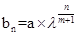 .
. ,所以
,所以 .
. ,所以
,所以 (*). 6分
(*). 6分 ,所以
,所以 为有理数.
为有理数.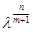 必须为有理数.
必须为有理数. ,所以
,所以 .
. ,则
,则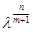 为无理数,不满足条件.
为无理数,不满足条件.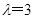 不满足条件. 8分
不满足条件. 8分 时,
时, .要使
.要使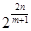 为有理数,则
为有理数,则 必须为整数.
必须为整数. ,所以仅有
,所以仅有 满足条件.
满足条件.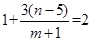 ,从而解得
,从而解得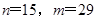 .
. 最小值为4,此时
最小值为4,此时 为29. 10分
为29. 10分 ,
, 为数列
为数列 的前
的前 项的和.
项的和. 为递增数列,则
为递增数列,则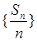 为递增数列.
为递增数列.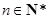 时,
时, .
.  ,所以
,所以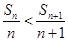 ,即数列
,即数列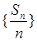 为递增数列.
为递增数列.  为递减数列,则
为递减数列,则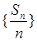 为递减数列. 12分
为递减数列. 12分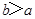 时,
时, .当
.当 时,
时,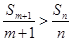 .
.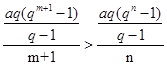 ,即
,即 .
. 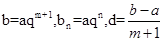 ,
, ,即
,即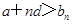 ,即
,即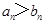 .
.  时,
时, ,当
,当 时,
时, .
. .
. ,所以
,所以 .以下同①.
.以下同①. . 16分
. 16分

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源:不详 题型:解答题
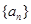 的首项
的首项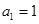 ,公差
,公差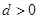 ,且第
,且第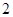 项、第
项、第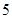 项、第
项、第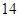 项分别是等比数列
项分别是等比数列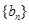 的第
的第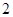 项、第
项、第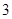 项、第
项、第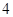 项.
项.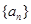 ,
,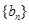 的通项公式;
的通项公式;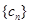 对任意
对任意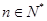 ,均有
,均有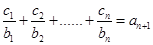 成立.
成立.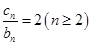 ; ②求
; ②求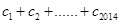 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 5 | 4 | 3 | 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

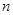 层
层 的点数为___________个;
的点数为___________个;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com