
ЁОЬтФПЁПФГЩЬГЁОйаагаНБДйЯњЛюЖЏЃЌЙЫПЭЙКТђУПТњ![]() дЊЕФЩЬЦЗМДПЩГщНБвЛДЮ.ГщНБЙцдђШчЯТЃКГщНБепжРИїУцБъга
дЊЕФЩЬЦЗМДПЩГщНБвЛДЮ.ГщНБЙцдђШчЯТЃКГщНБепжРИїУцБъга![]() ЕуЪ§ЕФе§ЗНЬхїЛзг
ЕуЪ§ЕФе§ЗНЬхїЛзг![]() ДЮЃЌШєжРЕУЕуЪ§Дѓгк
ДЮЃЌШєжРЕУЕуЪ§Дѓгк![]() ЃЌдђПЩМЬајдкГщНБЯфжаГщНБЃЛЗёдђЛёЕУШ§ЕШНБЃЌНсЪјГщНБЃЌвбжЊГщНБЯфжазАга
ЃЌдђПЩМЬајдкГщНБЯфжаГщНБЃЛЗёдђЛёЕУШ§ЕШНБЃЌНсЪјГщНБЃЌвбжЊГщНБЯфжазАга![]() ИіКьЧђгы
ИіКьЧђгы![]() ИіАзЧђЃЌГщНБепДгЯфжаШЮвтУўГі
ИіАзЧђЃЌГщНБепДгЯфжаШЮвтУўГі![]() ИіЧђЃЌШє
ИіЧђЃЌШє![]() ИіЧђОљЮЊКьЧђЃЌдђЛёЕУвЛЕШНБЃЌШє
ИіЧђОљЮЊКьЧђЃЌдђЛёЕУвЛЕШНБЃЌШє![]() ИіЧђЮЊ
ИіЧђЮЊ![]() ИіКьЧђКЭ
ИіКьЧђКЭ![]() ИіАзЧђЃЌдђЛёЕУЖўЕШНБЃЌЗёдђЃЌЛёЕУШ§ЕШНБЃЈГщНБЯфжаЕФЫљгааЁЧђЃЌГ§беЩЋЭтОљЯрЭЌЃЉ.
ИіАзЧђЃЌдђЛёЕУЖўЕШНБЃЌЗёдђЃЌЛёЕУШ§ЕШНБЃЈГщНБЯфжаЕФЫљгааЁЧђЃЌГ§беЩЋЭтОљЯрЭЌЃЉ.
![]() Шє
Шє![]() ЃЌЧѓЙЫПЭВЮМгвЛДЮГщНБЛюЖЏЛёЕУШ§ЕШНБЕФИХТЪЃЛ
ЃЌЧѓЙЫПЭВЮМгвЛДЮГщНБЛюЖЏЛёЕУШ§ЕШНБЕФИХТЪЃЛ
![]() ШєвЛЕШНБПЩЛёНБН№
ШєвЛЕШНБПЩЛёНБН№![]() дЊЃЌЖўЕШНБПЩЛёНБН№
дЊЃЌЖўЕШНБПЩЛёНБН№![]() дЊЃЌШ§ЕШНБПЩЛёНБН№
дЊЃЌШ§ЕШНБПЩЛёНБН№![]() дЊЃЌМЧЙЫПЭвЛДЮГщНБЫљЛёЕУЕФНБН№ЮЊ
дЊЃЌМЧЙЫПЭвЛДЮГщНБЫљЛёЕУЕФНБН№ЮЊ![]() ЃЌШєЩЬГЁЯЃЭћ
ЃЌШєЩЬГЁЯЃЭћ![]() ЕФЪ§бЇЦкЭћВЛГЌЙ§
ЕФЪ§бЇЦкЭћВЛГЌЙ§![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ЁОД№АИЁП![]()
![]() ЃЛ
ЃЛ![]()
![]() .
.
ЁОНтЮіЁП
![]() ЩшЙЫПЭЛёЕУШ§ЕШНБЮЊЪТМў
ЩшЙЫПЭЛёЕУШ§ЕШНБЮЊЪТМў![]() ЃЌвђЮЊЙЫПЭжРЕУЕуЪ§Дѓгк
ЃЌвђЮЊЙЫПЭжРЕУЕуЪ§Дѓгк![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]() ЃЌЙЫПЭжРЕУЕуЪ§аЁгк
ЃЌЙЫПЭжРЕУЕуЪ§аЁгк![]() ЃЌШЛКѓГщНЋЕУШ§ЕШНБЕФИХТЪЮЊ
ЃЌШЛКѓГщНЋЕУШ§ЕШНБЕФИХТЪЮЊ![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЛ
ЃЛ
![]() гЩЬтвтПЩжЊЃЌЫцЛњБфСП
гЩЬтвтПЩжЊЃЌЫцЛњБфСП![]() ЕФПЩФмШЁжЕЮЊ
ЕФПЩФмШЁжЕЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЯргІЧѓГіИХТЪЃЌЧѓГіЦкЭћЃЌЛЏМђЕУ
ЃЌЯргІЧѓГіИХТЪЃЌЧѓГіЦкЭћЃЌЛЏМђЕУ![]() ЃЌгЩЬтвтПЩжЊЃЌ
ЃЌгЩЬтвтПЩжЊЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
![]() ЩшЙЫПЭЛёЕУШ§ЕШНБЮЊЪТМў
ЩшЙЫПЭЛёЕУШ§ЕШНБЮЊЪТМў![]() ЃЌ
ЃЌ
вђЮЊЙЫПЭжРЕУЕуЪ§Дѓгк![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
ЙЫПЭжРЕУЕуЪ§аЁгк![]() ЃЌШЛКѓГщНЋЕУШ§ЕШНБЕФИХТЪЮЊ
ЃЌШЛКѓГщНЋЕУШ§ЕШНБЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЛ
ЃЛ
![]() гЩЬтвтПЩжЊЃЌЫцЛњБфСП
гЩЬтвтПЩжЊЃЌЫцЛњБфСП![]() ЕФПЩФмШЁжЕЮЊ
ЕФПЩФмШЁжЕЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Чв![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЫљвдЫцЛњБфСП![]() ЕФЪ§бЇЦкЭћЃЌ
ЕФЪ§бЇЦкЭћЃЌ
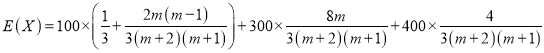 ЃЌ
ЃЌ
ЛЏМђЕУ![]() ЃЌ
ЃЌ
гЩЬтвтПЩжЊЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЛЏМђЕУ![]() ЃЌвђЮЊ
ЃЌвђЮЊ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
МД![]() ЕФзюаЁжЕЮЊ
ЕФзюаЁжЕЮЊ![]() .
.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕxOyжаЃЌжБЯпlЕФВЮЪ§ЗНГЬЪЧ![]() ЃЈtЪЧВЮЪ§ЃЉ.дквдOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌЧњЯп
ЃЈtЪЧВЮЪ§ЃЉ.дквдOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌЧњЯп![]() .
.
ЃЈ1ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓжБЯпlгыЧњЯпCЕФжБНЧзјБъЗНГЬЃЛ
ЪБЃЌЧѓжБЯпlгыЧњЯпCЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌШєжБЯпlгыЧњЯпCЯрНЛгкAЃЌBСНЕуЃЌЩш
ЪБЃЌШєжБЯпlгыЧњЯпCЯрНЛгкAЃЌBСНЕуЃЌЩш![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжБЯпlЕФЧуаБНЧ.
ЃЌЧѓжБЯпlЕФЧуаБНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
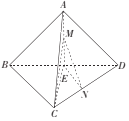
ЁОЬтФПЁПШчЭМЃЌдкШ§РтзЖAЉBCDжаЃЌЕуEдкBDЩЯЃЌEAЃНEBЃНECЃНEDЃЌBD![]() CDЃЌЁїACDЮЊе§Ш§НЧаЮЃЌЕуMЃЌNЗжБ№дкAEЃЌCDЩЯдЫЖЏЃЈВЛКЌЖЫЕуЃЉЃЌЧвAMЃНCNЃЌдђЕБЫФУцЬхCЉEMNЕФЬхЛ§ШЁЕУзюДѓжЕ
CDЃЌЁїACDЮЊе§Ш§НЧаЮЃЌЕуMЃЌNЗжБ№дкAEЃЌCDЩЯдЫЖЏЃЈВЛКЌЖЫЕуЃЉЃЌЧвAMЃНCNЃЌдђЕБЫФУцЬхCЉEMNЕФЬхЛ§ШЁЕУзюДѓжЕ![]() ЪБЃЌШ§РтзЖAЉBCDЕФЭтНгЧђЕФБэУцЛ§ЮЊ_____.
ЪБЃЌШ§РтзЖAЉBCDЕФЭтНгЧђЕФБэУцЛ§ЮЊ_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРюПЫЧПзмРэдк2018ФъеўИЎЙЄзїБЈИцжИГіЃЌвЊМгПьНЈЩшДДаТаЭЙњМвЃЌАбЮеЪРНчаТвЛТжПЦММИяУќКЭВњвЕБфИяДѓЪЦЃЌЩюШыЪЕЪЉДДаТЧ§ЖЏЗЂеЙеНТдЃЌВЛЖЯдіЧПОМУДДаТСІКЭОКељСІ.ФГЪжЛњЩњВњЦѓвЕЛ§МЋЯьгІеўИЎКХейЃЌДѓСІбаЗЂаТВњЦЗЃЌељДДЪРНчУћХЦ.ЮЊСЫЖдбаЗЂЕФвЛХњзюаТПюЪжЛњНјааКЯРэЖЈМлЃЌНЋИУПюЪжЛњАДЪТЯШФтЖЈЕФМлИёНјааЪдЯњЃЌЕУЕНвЛзщЯњЪлЪ§Он![]() ЃЌШчБэЫљЪОЃК
ЃЌШчБэЫљЪОЃК
ЕЅМл |
|
|
|
|
|
|
ЯњСП |
|
|
|
|
|
|
вбжЊ![]() .
.
ЃЈ1ЃЉШєБфСП![]() ОпгаЯпадЯрЙиЙиЯЕЃЌЧѓВњЦЗЯњСП
ОпгаЯпадЯрЙиЙиЯЕЃЌЧѓВњЦЗЯњСП![]() ЃЈАйМўЃЉЙигкЪдЯњЕЅМл
ЃЈАйМўЃЉЙигкЪдЯњЕЅМл![]() ЃЈЧЇдЊЃЉЕФЯпадЛиЙщЗНГЬ
ЃЈЧЇдЊЃЉЕФЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгУЃЈ1ЃЉжаЫљЧѓЕФЯпадЛиЙщЗНГЬЕУЕНгы![]() ЖдгІЕФВњЦЗЯњСПЕФЙРМЦжЕ
ЖдгІЕФВњЦЗЯњСПЕФЙРМЦжЕ![]() .ЕБЯњЪлЪ§Он
.ЕБЯњЪлЪ§Он![]() ЖдгІЕФВаВюЕФОјЖджЕ
ЖдгІЕФВаВюЕФОјЖджЕ![]() ЪБЃЌдђНЋЯњЪлЪ§Он
ЪБЃЌдђНЋЯњЪлЪ§Он![]() ГЦЮЊвЛИіЁАКУЪ§ОнЁБ.ЯжДг
ГЦЮЊвЛИіЁАКУЪ§ОнЁБ.ЯжДг![]() ИіЯњЪлЪ§ОнжаШЮШЁ
ИіЯњЪлЪ§ОнжаШЮШЁ![]() ИізгЃЌЧѓЁАКУЪ§ОнЁБИіЪ§
ИізгЃЌЧѓЁАКУЪ§ОнЁБИіЪ§![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ
ЕФЗжВМСаКЭЪ§бЇЦкЭћ![]() .
.
ЃЈВЮПМЙЋЪНЃКЯпадЛиЙщЗНГЬжа![]() ЕФЙРМЦжЕЗжБ№ЮЊ
ЕФЙРМЦжЕЗжБ№ЮЊ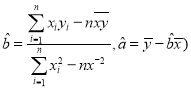 .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЧѓ![]() дк
дк![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧѓжЄЃК![]() гаЧвНігаСНИіСуЕу.
гаЧвНігаСНИіСуЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉ.вддЕу
ЮЊВЮЪ§ЃЉ.вддЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФЦеЭЈЗНГЬКЭ
ЕФЦеЭЈЗНГЬКЭ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() гы
гы![]() ЯрЧагкЕкЖўЯѓЯоЕФЕу
ЯрЧагкЕкЖўЯѓЯоЕФЕу![]() ЃЌгы
ЃЌгы![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЧуаБНЧ.
ЕФЧуаБНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЪЧБпГЄЮЊ4ЕФе§ЗНаЮЃЌ
ЪЧБпГЄЮЊ4ЕФе§ЗНаЮЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕу.
ЕФжаЕу.

ЃЈ1ЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() .
.
ЃЈ2ЃЉШє![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФе§ЯвжЕ.
ЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввСНМвЭтТєЙЋЫОЃЌЦфЫЭВЭдБЕФШеЙЄзЪЗНАИШчЯТЃКМзЙЋЫОЕзаН![]() дЊЃЌЫЭВЭдБУПЕЅжЦГЩ
дЊЃЌЫЭВЭдБУПЕЅжЦГЩ![]() дЊЃЛввЙЋЫОЮоЕзаНЃЌ
дЊЃЛввЙЋЫОЮоЕзаНЃЌ![]() ЕЅвдФкЃЈКЌ
ЕЅвдФкЃЈКЌ![]() ЕЅЃЉЕФВПЗжЫЭВЭдБУПЕЅГщГЩ
ЕЅЃЉЕФВПЗжЫЭВЭдБУПЕЅГщГЩ![]() дЊЃЌГЌЙ§
дЊЃЌГЌЙ§![]() ЕЅЕФВПЗжЫЭВЭдБУПЕЅГщГЩ
ЕЅЕФВПЗжЫЭВЭдБУПЕЅГщГЩ![]() дЊ.ЯжДгетСНМвЙЋЫОИїЫцЛњбЁШЁвЛУћЫЭВЭдБЃЌЗжБ№МЧТМЦф
дЊ.ЯжДгетСНМвЙЋЫОИїЫцЛњбЁШЁвЛУћЫЭВЭдБЃЌЗжБ№МЧТМЦф![]() ЬьЕФЫЭВЭЕЅЪ§ЃЌЕУЕНШчЯТЦЕЪ§ЗжВМБэЃК
ЬьЕФЫЭВЭЕЅЪ§ЃЌЕУЕНШчЯТЦЕЪ§ЗжВМБэЃК
ЫЭВЭЕЅЪ§ | 38 | 39 | 40 | 41 | 42 |
МзЙЋЫОЬьЪ§ | 10 | 10 | 15 | 10 | 5 |
ввЙЋЫОЬьЪ§ | 10 | 15 | 10 | 10 | 5 |
ЃЈ1ЃЉДгМЧТММзЙЋЫОЕФ![]() ЬьЫЭВЭЕЅЪ§жаЫцЛњГщШЁ
ЬьЫЭВЭЕЅЪ§жаЫцЛњГщШЁ![]() ЬьЃЌЧѓет
ЬьЃЌЧѓет![]() ЬьЕФЫЭВЭЕЅЪ§ЖМВЛаЁгк
ЬьЕФЫЭВЭЕЅЪ§ЖМВЛаЁгк![]() ЕЅЕФИХТЪЃЛ
ЕЅЕФИХТЪЃЛ
ЃЈ2ЃЉМйЩшЭЌвЛЙЋЫОЕФЫЭВЭдБвЛЬьЕФЫЭВЭЕЅЪ§ЯрЭЌЃЌНЋЦЕТЪЪгЮЊИХТЪЃЌЛиД№ЯТСаСНИіЮЪЬтЃК
ЂйЧѓввЙЋЫОЫЭВЭдБШеЙЄзЪЕФЗжВМСаКЭЪ§бЇЦкЭћЃЛ
ЂкаЁеХДђЫуЕНМзЁЂввСНМвЙЋЫОжаЕФвЛМвгІЦИЫЭВЭдБЃЌШчЙћНіДгШеЙЄзЪЕФНЧЖШПМТЧЃЌаЁеХгІбЁдёФФМвЙЋЫОгІЦИЃПУїФуЕФРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКЦНУцФкСНИіЗжБ№вддЕуКЭСНзјБъжсЮЊЖдГЦжааФКЭЖдГЦжсЕФЭждВE1ЃЌE2ЃЌЫќУЧЕФГЄЖЬАыжсГЄЗжБ№ЮЊa1ЃЌb1КЭa2ЃЌb2ЃЌШєТњзуa2=a1kЃЌb2=b1kЃЈkЁЪZЃЌkЁн2ЃЉЃЌдђГЦE2ЮЊE1ЕФkМЖЯрЫЦЭждВЃЌМКжЊЭждВE1: ![]() =1ЃЌE2ЮЊE1ЕФ2МЖЯрЫЦЭждВЃЌЧвНЙЕуЙВжсЃЌE1гыE2ЕФРыаФТЪжЎБШЮЊ2ЃК
=1ЃЌE2ЮЊE1ЕФ2МЖЯрЫЦЭждВЃЌЧвНЙЕуЙВжсЃЌE1гыE2ЕФРыаФТЪжЎБШЮЊ2ЃК![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓE2ЕФЗНГЬЃЛ
ЃЈЂђЃЉвбжЊPЮЊE2ЩЯШЮвтвЛЕуЃЌЙ§ЕуPзїE1ЕФСНЬѕЧаЯпЃЌЧаЕуЗжБ№ЮЊA(x1ЃЌy1)ЁЂB(x2ЃЌy2)ЃЎ
ЂйжЄУїЃКE1дкA(x1ЃЌy1)ДІЕФЧаЯпЗНГЬЮЊ![]() =1ЃЛ
=1ЃЛ
ЂкЪЧЗёДцдквЛЖЈЕуЕНжБЯпABЕФОрРыЮЊЖЈжЕЃЌШєДцдкЃЌЧѓГіИУЖЈЕуКЭЖЈжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com