
分析 由题意可得t=x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{8}$),题目转化为y=Acosωt在t∈($\frac{π}{4}$,$\frac{3π}{8}$)上是减函数,由余弦函数的图象和周期公式可得ω的不等式,解不等式可得.
解答 解:∵x∈(0,$\frac{π}{8}$),∴t=x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{8}$),
∴y=Acosω(x+$\frac{π}{4}$)=Acosωt在t∈($\frac{π}{4}$,$\frac{3π}{8}$)上是减函数,
∴ω>0且$\frac{1}{2}$•$\frac{2π}{ω}$≥$\frac{3π}{8}$,解得0<ω≤$\frac{8}{3}$,
∴ω的最大值为$\frac{8}{3}$
点评 本题考查余弦函数的图象和性质,涉及周期公式和换元的思想,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10250 | B. | 3430 | C. | 825 | D. | 405 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$x-y-4=0 | B. | $\sqrt{3}$x+y-2=0 | C. | $\sqrt{3}$x-y-2=0 | D. | $\sqrt{3}$x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
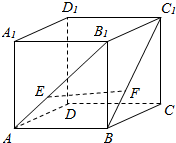 如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,正方体ABCD-A1B1C1D1,E,F分别在AB1,BC1上,且$\frac{{B}_{1}E}{AE}$=$\frac{{C}_{1}F}{BF}$=2,过EF做一个平面和面ABCD相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com