练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设a，b是两个单位向量，命题p：“（2a+b）⊥b”是命题a：“a•b”的夹角等于数学公式成立的


    1. A.
      充分不必要条件
    2. B.
      必要不充分条件
    3. C.
      充要条件
    4. D.
      既不充分也不必要条件
    C
    分析：利用向量垂直的充要条件列出方程；利用向量的数量积公式得到两个向量的夹角；利用充要条件的定义得到选项．
    解答：∵??
    ∵是两个单位向量
    ∴??的夹角为
    故选C．
    点评：本题考查两个向量垂直的充要条件、向量的数量积公式、充要条件的定义．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2009•济宁一模）给出下列四个命题：
    ①命题：“设a，b∈R，若ab=0，则a=0或b=0”的否命题是“设a，b∈R，若ab≠0，则a≠0且b≠0”； 
    ②将函数y=
    		2
    sin（2x+
    π
    4
    ）的图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），再向右平移
    π
    4
    个单位长度，得到函数y=
    		2
    cosx的图象； 
    ③用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•2•3…（2n-1）（n∈N*）时，从“k”到“k+1”的证明，左边需增添的一个因式是2（2k+1）； 
    ④函数f（x）=ex-x-1（x∈R）有两个零点．
    其中所有真命题的序号是
    ①③
    ①③
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    选择题：

    (1)如果a，b是两个单位向量，那么下列四个结论中正确的是

    [　　]

    (A)a＝b

    (B)a·b＝1

    (C)

    (D)

    (2)对于任意向量a、b，下列命题中正确的是

    [　　]

    (A)若a，b满足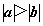，且a与b同向，则a＞b

    (B)

    (C)

    (D)

    (3)在四边形ABCD中，若，则

    [　　]

    (A)ABCD是矩形

    (B)ABCD是菱形

    (C)ABCD是正方形

    (D)ABCD是平行四边形

    (4)设a是非零向量，λ是非零实数，下列结论中正确的是

    [　　]

    (A)a与－λa的方向相反

    (B)

    (C)a与的方向相同

    (D)

    (5)设M是□ABCD的对角线的交点，O为任意一点，则等于

    [　　]

    (A)

    (B)2

    (C)3

    (D)4

    (6)下列各组向量中，可以作为基底的是

    [　　]

    (A)，

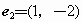
    (B)，

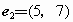
    (C)，

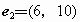
    (D)，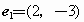

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设i,j是平面直角坐标系内分别与x轴，y轴正方向相同的两个单位向量,O为坐标原点，若=4i+2j, =3i+4j,则2+的坐标是(    )

    A．（1，-2） B．（7，6）  C．（5，0）   D．（11，8）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设i，j是平面直角坐标系内分别与x轴，y轴正方向相同的两个单位向量，O为坐标原点，若=4i+2j, =3i+4i,则2+的坐标是（    ）

    A.（1，－2）                           B.（7，6）

    C.（5，0）                             D.（11，8）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年贵州省黔西南州册亨一中高三（上）9月月考数学试卷（文科）（解析版） 题型：选择题

    设函数y=f（x）的反函数为f-1（x），将y=f（2x-3）的图象向左平移两个单位，再关于x轴对称后所得到的函数的反函数是（ ）
    A．
    B．
    C．
    D．

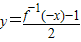
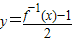
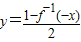
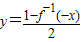
    查看答案和解析>>

    同步练习册答案