解:(1)f′(x)=3x
2-6x+2…(1分)f″(x)=6x-6令f″(x)=6x-6=0得x=1…(2分)f(1)=1
3-3+2-2=-2∴拐点A(1,-2)…(3分)
(2)设P(x
0,y
0)是y=f(x)图象上任意一点,则y
0=x
03-3x
02+2x
0-2,因为P(x
0,y
0)关于A(1,-2)的对称点为P'(2-x
0,-4-y
0),
把P'代入y=f(x)得左边=-4-y
0=-x
03+3x
02-2x
0-2
右边=(2-x
0)
3-3(2-x
0)
2+2(2-x
0)-2=-x
03+3x
02-2x
0-2∴右边=右边∴P′(2-x
0,-4-y
0)在y=f(x)图象上∴y=f(x)关于A对称 …(7分)
结论:①任何三次函数的拐点,都是它的对称中心
②任何三次函数都有“拐点”
③任何三次函数都有“对称中心”(写出其中之一)…(9分)
(3)设G(x)=ax
3+bx
2+d,则G(0)=d=1…(10分)∴G(x)=ax
3+bx
2+1,G'(x)=3ax
2+2bx,G''(x)=6ax+2bG''(0)=2b=0,b=0,∴G(x)=ax
3+1=0…(11分)
法一:

=

=
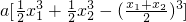
=
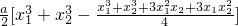
=

=
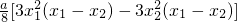
=
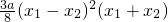
…(13分)
当a>0时,

当a<0时,

…(14分)
法二:G′′(x)=3ax,当a>0时,且x>0时,G′′(x)>0,∴G(x)在(0,+∞)为凹函数,∴

…(13分)
当a<0时,G′′(x)<0,∴G(x)在(0,+∞)为凸函数∴

…(14分)
分析:(1)先求f′(x)得解析式,再求f″(x),由f″(x)=0 求得拐点的横坐标,代入函数解析式求拐点的坐标.
点评:本题考查一阶导数、二阶导数的求法,函数的拐点的定义以及函数图象关于某点对称的条件.属于中档题.

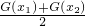 与
与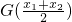 的大小.
的大小. =
= =
=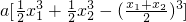 =
=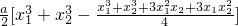 =
= =
=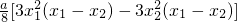 =
=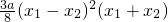 …(13分)
…(13分)
 …(14分)
…(14分) …(13分)
…(13分) …(14分)
…(14分)
