
【题目】甲乙两名射击运动员分别对一目标射击一次,甲射中的概率为0.8,乙射中的概率为0.9,求:
(1)2人都射中目标的概率;
(2)2人中恰有1人射中目标的概率;
(3)2人至少有1人射中目标的概率。
【答案】(1)![]() ,(2)
,(2)![]() .(3)
.(3)![]() .
.
【解析】
(1)只需将两人射中的概率相乘即可,(2)恰有一人射中则包括甲击中、乙未击中和甲未击中、乙击中,分别求出对应的概率再相加即可,(3)可根据对立事件先将两人都不射中的概率求出,在用1减去两人都不中的情况即得结论.
记“甲射击![]() 次,击中目标”为事件
次,击中目标”为事件![]() ,“乙射击
,“乙射击![]() 次,击中目标”为事件
次,击中目标”为事件![]() ,则
,则![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() ,
,![]() 与
与![]() 为相互独立事件,
为相互独立事件,
(1)![]() 人都射中的概率为:
人都射中的概率为:
![]() ,
,
∴![]() 人都射中目标的概率是
人都射中目标的概率是![]() .
.
(2)“![]() 人各射击
人各射击![]() 次,恰有
次,恰有![]() 人射中目标”包括两种情况:一种是甲击中、乙未击中(事件
人射中目标”包括两种情况:一种是甲击中、乙未击中(事件![]() 发生),另一种是甲未击中、乙击中(事件
发生),另一种是甲未击中、乙击中(事件![]() 发生)根据题意,事件
发生)根据题意,事件![]() 与
与![]() 互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
互斥,根据互斥事件的概率加法公式和相互独立事件的概率乘法公式,所求的概率为:
![]()
![]()
∴![]() 人中恰有
人中恰有![]() 人射中目标的概率是
人射中目标的概率是![]() .
.
(3)(法1):2人至少有1人射中包括“2人都中”和“2人有1人不中”2种情况,其概率为![]() .
.
(法2):“2人至少有一个击中”与“2人都未击中”为对立事件,
2个都未击中目标的概率是![]() ,
,
∴“两人至少有1人击中目标”的概率为![]() .
.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述错误的的是_____________.
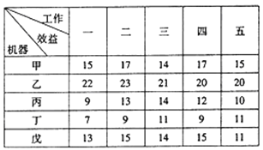
①甲只能承担第四项工作
②乙不能承担第二项工作
③丙可以不承担第三项工作
④丁可以承担第三项工作
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=![]() ,
,
(1)求f(x)的最小值;
(2)对任意![]() ,
,![]() 都有恒成立,求实数a的取值范围;
都有恒成立,求实数a的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
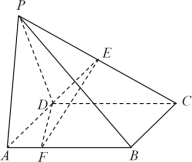
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)设二面角![]() 的平面角为
的平面角为![]() ,试判断在线段
,试判断在线段![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com