
| A. | 2 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -2 |
分析 利用递推公式求出数列的前5项,得到数列{an}是以4为周期的周期数列,由此能求出该数列的前2017项的乘积a1a2a3…a2017.
解答 解:∵数列{an}满足${a_1}=2,{a_{n+1}}=\frac{{{a_n}-1}}{{{a_n}+1}}(n∈N*)$,
∴${a}_{2}=\frac{2-1}{2+1}$=$\frac{1}{3}$,
${a}_{3}=\frac{\frac{1}{3}-1}{\frac{1}{3}+1}$=-$\frac{1}{2}$,
${a}_{4}=\frac{-\frac{1}{2}-1}{-\frac{1}{2}+1}$=-3,
${a}_{5}=\frac{-3-1}{-3+1}$=2.
∴数列{an}是以4为周期的周期数列,
∴该数列的前2017项的乘积a1a2a3…a2017=(a1a2a3a4)504•(a1a2a3)=[$2×\frac{1}{3}×(-\frac{1}{2})×(-3)$]504×[2×$\frac{1}{3}×(-\frac{1}{2})$]=-$\frac{1}{3}$.
故选:C.
点评 本题考查数列的前2017项积的求法,是中档题,解题时要认真审题,注意数列的递推公式的合理运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | y=x-1 | C. | y=($\frac{1}{2}$)x | D. | y=x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
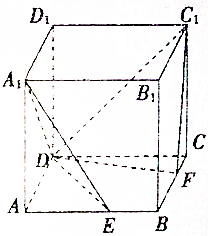 如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E,F分别是棱AB,BC上的动点,且AE=BF.当A1,E,F,C1共面时,平面A1DE与平面C1DF所成锐二面角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | $\frac{2\sqrt{6}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com