
【题目】已知函数![]() .
.
(1)若函数![]() 是函数
是函数![]() 的反函数,解方程
的反函数,解方程![]() ;
;
(2)当![]()
![]() 时,定义
时,定义![]() ,设
,设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 及
及![]() ;
;
(3)对于任意![]() ,其中
,其中![]() ,当
,当![]() 能作为一个三角形的三边长时,
能作为一个三角形的三边长时,![]() 也总能作为一个三角形的三边长,试探究M的最小值.
也总能作为一个三角形的三边长,试探究M的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)最小值为2.
;(3)最小值为2.
【解析】
(1)由题设知g(x)![]() ,f﹣1(x)=2x,由g(2x)=3f﹣1(x)+3,得
,f﹣1(x)=2x,由g(2x)=3f﹣1(x)+3,得![]() ,由此能求出原方程的解;
,由此能求出原方程的解;
(2)若1∈(3m,3m+3],m=0,能导出a1=0;若2∈(3m,3m+3],m=0,能导出a2=2;若3∈(3m,3m+3],m=0,能导出a3=3log23;若4∈(3m,3m+3],m=1,能导出a4=0;当n=3m+1(m∈N)时,能导出an=0;当n=3m+2(m∈N)时,能导出an=n;当n=3m+3(m∈N)时,能导出an=nlog23.由此能求出S3n;
(3)由题意知,c+b>a,若f(a),f(b),f(c)能作为某个三角形的三边长log2c+log2b>log2abc>a,bc≥b+c(b﹣1)(c﹣1)≥1.当b≥2,c≥2时,有(b﹣1)(c﹣1)≥1成立,则一定有bc>a成立.由此能够得出M的最小值为2.
(1)∵函数y=g(x)是函数y=f(2x+1)的反函数,
∴g(x)![]() ,f﹣1(x)=2x,
,f﹣1(x)=2x,
∵g(2x)=3f﹣1(x)+3,∴![]() ,
,
解得2x=7,∴x=log27.
(2)若1∈(3m,3m+3],∴m=0,∴φ(1)=f(1)=0,∴a1=1×0=0
若2∈(3m,3m+3],∴m=0,∴φ(2)=f(2)=1,∴a2=2×1=2
若3∈(3m,3m+3],∴m=0,∴φ(3)=f(3)=log23,∴a3=3log23
若4/span>∈(3m,3m+3],∴m=1,∴φ(4)=f(1)=0,∴a4=4×0=0
当n=3m+1(m∈N)时,φ(n)=f(n﹣3m)=f(1)=0,∴an=n×0=0
当n=3m+2(m∈N)时,φ(n)=f(n﹣3m)=f(2)=1,∴an=n×1=n
当n=3m+3(m∈N)时,φ(n)=f(n﹣3m)=f(3)=log23,
∴an=nlog23,
S3n=a1+a2+a3+a4+…+a3n
=1×0+2×1+3×log23+4×0+5×1+…+3nlog23
=(2+5+8+…+3n﹣1)×1+(3+6+9+…+3n)log23
![]() n
n![]() n×log23
n×log23
![]() [3n+1+(3n+3)log23].
[3n+1+(3n+3)log23].
(3)a、b、c能作为一个三角形的三边长,由题意知,c+b>a
∵f(a),f(b),f(c)能作为某个三角形的三边长,
∴log2c+log2b>log2a,
∴bc>a,
当b≥2,c≥2时,有(b﹣1)(c﹣1)≥1成立,则一定有bc>a成立.
∵log2c>0,
∴c>1,即0<M≤1不合题意.
又当1<M<2时,取b=M,c=M,a=M2,有M+M>M2,即b+c>a,
此时a,b,c可作为一个三角形的三边长,但log2M+log2M=2log2M=log2M2,
即f(b)+f(c)=f(a),所以f(a)、f(b)、f(c)不能作为三角形的三边长.
综上所述,M的最小值为2.


科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为A(A为常数)元,之后每年会投入一笔研发资金,n年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() ,
,![]() 为常数,
为常数,![]() .已知3年后总投入资金为研发启动是投入资金的3倍,问:
.已知3年后总投入资金为研发启动是投入资金的3倍,问:
(1)研发启动多少年后,总投入资金是研发启动时投入资金的8倍;
(2)研发启动后第几年投入的资金最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,下表是对100辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
分组 | 频数 |
| 6 |
| 10 |
| 20 |
| 30 |
| 18 |
| 12 |
| 4 |
(1)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(2)用分层抽样的方法从行车里程在区间![]() 与
与![]() 的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在
的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
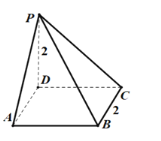
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com