
分析 先利用和角公式,倍角公式,将函数f(x)化为正弦型函数的形式;
(1)令2x+$\frac{π}{3}$∈[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z,可得函数f(x)的单调递减区间;
(2)将函数f(x)的图象向右平移m个单位,使所得函数为偶函数,则-2m+$\frac{π}{3}$=$\frac{π}{2}$+kπ,k∈Z,进而得到答案.
解答 解:f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx
=2cosx•(sinxcos$\frac{π}{3}$+cosxsin$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx
=2sinxcosx+$\sqrt{3}$cos2x-$\sqrt{3}$sin2x
=sin2x+$\sqrt{3}$cos2x
=2sin(2x+$\frac{π}{3}$)…3分;
(1)令2x+$\frac{π}{3}$∈[$\frac{π}{2}$+2kπ,$\frac{3π}{2}$+2kπ],k∈Z得:x∈[$\frac{π}{12}$+kπ,$\frac{7π}{12}$+kπ],k∈Z,
即函数f(x)的单调递减区间为[$\frac{π}{12}$+kπ,$\frac{7π}{12}$+kπ],k∈Z,…6分;
(2)(2)将函数f(x)的图象向右平移m个单位,
可得函数g(x)=2sin(2x-2m+$\frac{π}{3}$)的图象…9分
∵函数为偶函数,
故-2m+$\frac{π}{3}$=$\frac{π}{2}$+kπ,k∈Z,
当k=-1时,m取最小正值$\frac{5π}{12}$…12分
点评 本题考查的知识点是三角函数中的恒等变换,正弦函数的图象和性质,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,D1D=DC=4,AD=2,E为D1C的中点.
如图,长方体ABCD-A1B1C1D1中,D1D=DC=4,AD=2,E为D1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
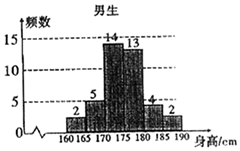 为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com