
【题目】设 ![]() ,若0≤a≤1,n∈N+且n≥2,求证:f(2x)≥2f(x).
,若0≤a≤1,n∈N+且n≥2,求证:f(2x)≥2f(x).
 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】为了丰富退休生活,老王坚持每天健步走,并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数(老王每天健步走的步数都在![]() 之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
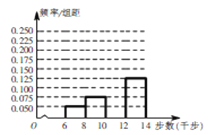
(1)完成频率分布直方图,并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替;
(2)某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天,求这2天的健步走结果属于同一评价级别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,若截面PQMN是正方形,则在下列命题中,错误的为( ) 
A.AC⊥BD
B.AC=BD
C.AC∥截面PQMN
D.异面直线PM与BD所成的角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线m、n与平面α、β,下列命题正确的是( )
A.m⊥α,n∥β且α⊥β,则m⊥n
B.m⊥α,n⊥β且α⊥β,则m⊥n
C.α∩β=m,n⊥m且α⊥β,则n⊥α
D.m∥α,n∥β且α∥β,则m∥n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项均为正数的数列,{bn}是等差数列,且a1=b1=1,a5﹣3b2=7.2a ![]() +(2﹣an+1)an﹣an+1=0(n∈N*)
+(2﹣an+1)an﹣an+1=0(n∈N*)
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数字![]() 组成没有重复数字的四位数.
组成没有重复数字的四位数.
(Ⅰ)可组成多少个不同的四位数?
(Ⅱ)可组成多少个不同的四位偶数?
(Ⅲ)将(Ⅰ)中的四位数按从小到大的顺序排成一数列,问第![]() 项是什么?
项是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com