Question

已知c=3，
（I）A={1，2，3，4，5}，在集合A中任取元素分别作为a，b的值（a，b的值可以相等，也可以不相等），求以a，b，c为三边长且能构成三角形的概率；
（II）B=[1，5]，在区间B中任取元素分别作为a，b的值（a，b的值可以相等也可以不相等），求以a，b，c为三边长且能构成三角形的概率．

Answer 1

分析：（Ⅰ）把（a，b）看成一个基本事件，则基本事件总数有25个，满足条件|a-b|≥3或a+b≤3的基本事件有9个，这9个都不能构成三角形，最后利用对立事件得到能构成三角形的概率．
（Ⅱ）a，b，c能构成三角形的充要条件是

1＜a＜5 1＜b＜5 |a-b＜3 a+b＞3

，在坐标系aob内画出满足以上条件的区域，如图所示，根据几何概型的计算方法即可求得结果．

解答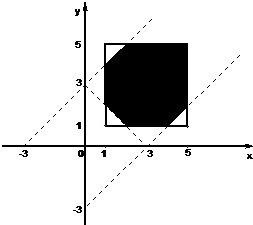：解：（Ⅰ）把（a，b）看成一个基本事件，则基本事件总数有25个，满足条件|a-b|≥3或a+b≤3的基本事件有9个，这9个都不能构成三角形，所以能构成三角形的概率为P=1-

9

25

=

16

25

．…（5分）
（Ⅱ）以a，b，c为三边长，能构成三角形
则a，b满足关系：

1＜a＜5 1＜b＜5 |a-b＜3 a+b＞3

，它表示的平面区域如图所示，…（8分）
所以，所球的概率为：P=1-

1.5

16

=

29

32

．…（10分）

点评：本题考查古典概型和几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=

N(A)

N

求解．属中档题．