
����Ŀ��Ϊ��߲�Ʒ������ij��ҵ�����������ž��������ڵس���Ʒ���м�⣬����ij���������������ȡ100����Ʒ����������ݵĶԱȣ�����ÿ����Ʒ�����ۺ����֣�����100�֣�����ÿ����Ʒ���õ��ۺ������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.���ۺ�����Ϊ80�ּ����ϵIJ�ƷΪһ��Ʒ.
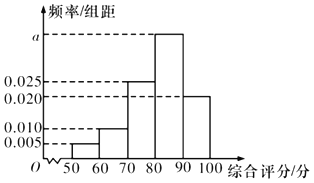
��1����ͼ��![]() ��ֵ�������ۺ����ֵ���λ����
��ֵ�������ۺ����ֵ���λ����
��2���������������壬��Ƶ����Ϊ���ʣ����ֲ������˼�룬���ڸ����������������ȡ5����Ʒ���ٴ���5����Ʒ�������ȡ2����Ʒ��¼�й����ݣ�����2����Ʒ��ǡ��һ��һ��Ʒ�ĸ���.
���𰸡�(1) ![]() ����λ��Ϊ82.5. (2)
����λ��Ϊ82.5. (2) ![]()
��������
��1������Ƶ��֮��Ϊ1�����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�������������⼴�ɣ��Ƚ����ֵԤ����λ���������Ӧ��80��90֮�䣬���ۺ����ֵ���λ��Ϊ![]() �����Ƶ�ʼ��㹫ʽ��⼴�ɣ�
�����Ƶ�ʼ��㹫ʽ��⼴�ɣ�
��2���Ƚ�Ϸֲ���������һ��Ʒ��ռ�������ٲ����оٷ���ʾ�����л����¼�����Ϲŵ���ʹ�ʽ��⼴��
��1����Ƶ�ʺ�Ϊ1����![]() ��
��![]() ��
��
���ۺ����ֵ���λ��Ϊ![]() ����
����![]() �����
�����![]() ��
��
�����ۺ����ֵ���λ��Ϊ82.5.
��2����Ƶ�ʷֲ�ֱ��ͼ֪��һ��Ʒ��Ƶ��Ϊ![]() ��������Ϊ0.6��
��������Ϊ0.6��
����100����Ʒ��һ��Ʒ��60������һ��Ʒ��40������һ��Ʒ���һ��Ʒ�ij�����Ϊ3��2��
�����ֳ�ȡ5����Ʒ��һ��Ʒ��3������Ϊ![]() ��
��![]() ��
��![]() ����һ��Ʒ2������Ϊ
����һ��Ʒ2������Ϊ![]() ��
��![]() ��
��
����5����Ʒ�������ȡ2���������¼�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��10�֣�
��10�֣�
��ȡ����2����Ʒ��ǡ��һ��һ��Ʒ���¼�Ϊ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��6�֣�
��6�֣�
��������ĸ���Ϊ![]() .
.


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ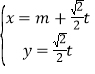 ��
��![]() Ϊ��������������ԭ��
Ϊ��������������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ����Բ
��������Ϊ���Ὠ��������ϵ����Բ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() ��ֱ��
��ֱ��![]() ��.
��.
��1����ֱ��![]() ����Բ
����Բ![]() ����
����![]() ���㣬��
���㣬��![]() ��ֵ��
��ֵ��
��2������Բ![]() ���ڽӾ�����������ֵ.
���ڽӾ�����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ����⣺
��![]() ��
��![]() ��
��![]() �����ij�Ҫ������
�����ij�Ҫ������
�ڵ�![]() ʱ����
ʱ����![]() ��
��
����֪![]() �ǵȲ�����
�ǵȲ�����![]() ��ǰn��ͣ���
��ǰn��ͣ���![]() ����
����![]() ��
��
��������![]() Ϊ
Ϊ![]() �ϵ��溯��������
�ϵ��溯��������![]() ��ͼ��һ�����ڵ�
��ͼ��һ�����ڵ�![]() �����ĶԳƣ�����������ȷ��������Ϊ___________��
�����ĶԳƣ�����������ȷ��������Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�A��B���������ֱ�Ϊ��0��1������0����1��������P����ֱ��AP��ֱ��BP��б��֮��Ϊ![]() ��ֱ��AP��BP��ֱ��y����2�ֱ��ڵ�M��N��
��ֱ��AP��BP��ֱ��y����2�ֱ��ڵ�M��N��
��1����P�Ĺ켣���̣�
��2�����߶�MN����Сֵ��
��3����MNΪֱ����Բ�Ƿ�ij���㣿���������㣬�����������ꣻ�����������㣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��ܾ�Ϊ���˽��������2018��1����2019��1���ڼ乺����ַ���������������������200�������ߣ������乺�����m����λ��ƽ���ף�![]() ��������һ�ε���ͳ�ƣ��Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
��������һ�ε���ͳ�ƣ��Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
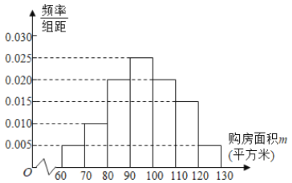
�����Թ��Ƹ��������ƽ�����������
�����ֲ��÷ֲ�����ķ����ӹ������λ��![]() ��40λ���������ȡ4�ˣ��ٴ���4���������ȡ2�ˣ�����2�˵Ĺ������ǡ����һ����
��40λ���������ȡ4�ˣ��ٴ���4���������ȡ2�ˣ�����2�˵Ĺ������ǡ����һ����![]() �ĸ��ʣ�
�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����![]() ��
��
��1�����ۺ���![]() �ĵ����ԣ���д����Ӧ�ĵ������䣻
�ĵ����ԣ���д����Ӧ�ĵ������䣻
��2����֪![]() ��
��![]() ����
����![]() ������
������![]() ����������
����������![]() �����ֵ��
�����ֵ��
��3����![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������
��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ��������״����ijУ�����ȡ��һ��ѧ����������.��ͳ�ƣ�����ѧ������������(��λ��ǧ��)ȫ������45��70֮��.�����ݷֳ�����5�飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���ֲ��÷ֲ�����ķ������ӵ�3��4��5���������ȡ6��ѧ�������3��4��5���ȡ��ѧ����������Ϊ�� ��
���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���ֲ��÷ֲ�����ķ������ӵ�3��4��5���������ȡ6��ѧ�������3��4��5���ȡ��ѧ����������Ϊ�� ��
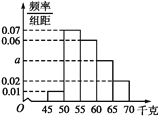
A.4��5��6B.3��2��1C.2��4��5D.2��1��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϸ�����ϱ��е�![]() վ�����ӿ�ʼλ�ڵ�
վ�����ӿ�ʼλ�ڵ�![]() վ��ѡ�������������ӽ�����Ϸ���������������ϵĵ���������
վ��ѡ�������������ӽ�����Ϸ���������������ϵĵ���������![]() ��������ǰ����һվ������������ǰ������վ��ֱ��������
��������ǰ����һվ������������ǰ������վ��ֱ��������![]() վ���
վ���![]() վʱ����Ϸ����.����Ϸ���������ӳ����ڵ�
վʱ����Ϸ����.����Ϸ���������ӳ����ڵ�![]() վ�ĸ���Ϊ
վ�ĸ���Ϊ![]() .
.
��1������Ϸ��ʼʱ����������������![]() �κ�����������վ��֮��
�κ�����������վ��֮��![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
��2��֤��:![]() ��
��
��3���������������ڵ�![]() վ�����ѡ����ܣ��������������ڵ�
վ�����ѡ����ܣ��������������ڵ�![]() վ�����ѡ�ֻ�ʤ.����������Ϸ�Ƿ�ƽ.
վ�����ѡ�ֻ�ʤ.����������Ϸ�Ƿ�ƽ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com