
【题目】已知f(x)是定义在R上的奇函数,当x∈[0,+∞)时,f(x)=2x+x﹣m(m为常数).
(1)求常数m的值.
(2)求f(x)的解析式.
(3)若对于任意x∈[﹣3,﹣2],都有f(k4x)+f(1﹣2x+1)>0成立,求实数k的取值范围.
【答案】
(1)解:∵f(x)是奇函数,且定义域为R;
∴f(0)=0;
∵当x≥0时,f(x)=2x+x﹣m(m为常数);
∴f(0)=1﹣m,∴1﹣m=0;
∴m=1
(2)解:由(1)知,m=1;
∴当x≥0时,f(x)=2x+x﹣1;
设x<0,则﹣x>0,且f(x)为奇函数,所以:
f(﹣x)=2﹣x﹣x﹣1=﹣f(x);
∴f(x)=﹣2﹣x+x+1;
∴ ![]()
(3)解:因为当x变大时,2x变大,x﹣1变大,所以2x+x﹣1的值也变大;
所以f(x)在[0,+∞)上是增函数且左端点为原点;
因为,f(x)是奇函数,且f(0)=0;
所以f(x)在(﹣∞,0)上也是增函数,且右端点是原点;
所以f(x)在R上是增函数;
∵f(x)是奇函数;
∴f(k4x)+f(1﹣2x+1)>0等价于f(k4x)>﹣f(1﹣2x+1),等价于f(k4x)>f(﹣1+2x+1);
∵f(x)在R上是增函数;
∴f(k4x)>f(﹣1+2x+1)等价于k4x>﹣1+2x+1;
∵4x>0∴k4x>﹣1+2x+1等价于 ![]() ;
;
∴f(k4x)+f(1﹣2x+1)>0对x∈[﹣3,﹣2]恒成立等价于 ![]() ;
;
设y= ![]() ;
;
∴ ![]() =
= ![]() ;
;
x∈[﹣3,﹣2],∴ ![]() ;
;
∴ ![]() 时,y取最大值﹣8;
时,y取最大值﹣8;
∴k>﹣8;
即实数k的取值范围为(﹣8,+∞).
【解析】1、本题考查的是奇函数的定义,且定义域为R∴f(0)=0,再由特殊之法求得m=1。
2、当x≥0时,f(x)=2x+x﹣1;x<0,则﹣x>0,且f(x)为奇函数,所以f(﹣x)=2﹣x﹣x﹣1=﹣f(x)∴f(x)=﹣2﹣x+x+1;即得函数的解析式。
3、由增函数的定义可得f(x)在R上是增函数∵f(x)是奇函数可得f(k4x)>f(﹣1+2x+1),根据增减性可得不等式k4x>﹣1+2x+1 ∴f(k4x)+f(1﹣2x+1)>0对x∈[﹣3,﹣2]恒成立,整理得![]() , x ∈ [ 3 , 2 ].整理得
, x ∈ [ 3 , 2 ].整理得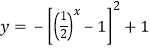 ,x∈[﹣3,﹣2],
,x∈[﹣3,﹣2],
∴ ![]() x ∈ [ 4 , 8 ] ,当
x ∈ [ 4 , 8 ] ,当![]() =4时,y取最大值﹣8∴k>﹣8
=4时,y取最大值﹣8∴k>﹣8
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某加工厂用某原料由车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天功能完成至多70多箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天获利最大的生产计划为( )
A.甲车间加工原料10箱,乙车间加工原料60箱
B.甲车间加工原料15箱,乙车间加工原料55箱
C.甲车间加工原料18箱,乙车间加工原料50箱
D.甲车间加工原料40箱,乙车间加工原料30箱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证: 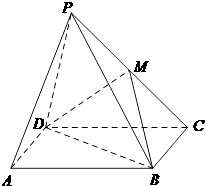
(1)PA∥平面MDB;
(2)PD⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场种植黄瓜,根据多年的市场行情得知,从春节起的300天内,黄瓜市场售价与上市时间的关系用图1所示的一条折线表示,黄瓜的种植成本与上市时间的关系用图2所示的抛物线表示.(注:市场售价和种植成本的单位:元/kg,时间单位:天)
(1)写出图1表示的市场售价与时间的函数关系式P=f(t);写出图2表示的种植成本与时间的函数关系式Q=g(x);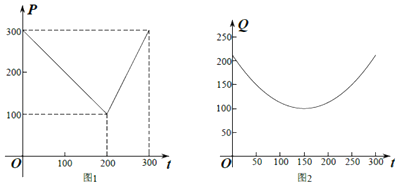
(2)认定市场售价减去种植成本为纯收益,问从春节开始的第几天上市的黄瓜纯收益最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={y|y=x2﹣2x﹣3,x∈R},B={x|log2x<﹣1},C={k|函数f(x)= ![]() 在(0,+∞)上是增函数}.
在(0,+∞)上是增函数}.
(1)求A,B,C;
(2)求A∩C,(UB)∪C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,p是q的充分不必要条件的是( ) ①p:m<﹣2或m>6,q:y=x2+mx+m+3有两个零点;
② ![]() ,q:y=f(x)是偶函数;
,q:y=f(x)是偶函数;
③p:cosα=cosβ,q:tanα=tanβ;
④p:A∩B=A,q:(UB)(UA)
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2ax+a2﹣1.
(1)若对任意的x∈R均有f(1﹣x)=f(1+x),求实数a的值;
(2)当x∈[﹣1,1]时,求f(x)的最小值,用g(a)表示其最小值,判断g(a)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=4,点E、F分别为AB和PD的中点. 
(1)求证:直线AF∥平面PEC;
(2)求平面PAD与平面PEC所成锐二面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com