Question

一条直线l被两条直线4x+y+6=0和3x-5y-6=0截得的线段的中点恰好是坐标原点,求直线l的方程.

Answer 1

思路分析:设直线l的方程为y=kx,与已知的两直线的交点设为P₁(x₁,y₁)、P₂(x₂,y₂),把x₁、x₂用k表示,由x₁+x₂=0,解出k的值即可.

解法一:当直线l的斜率k存在时,设l的方程为y=kx,且l与已知两直线的交点分别为P₁(x₁,y₁)、P₂(x₂,y₂),

则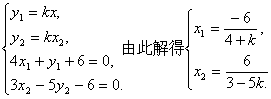

因为O是P₁P₂的中点,所以x₁+x₂=0,

即=0,解得k=.

当斜率k不存在时,直线l是y轴,它和两条已知直线的交点分别是(0,-6)和(0,),显然不满足中点是原点的条件.

所以所求的直线方程为y=x.

解法二:设过原点的直线l交已知两直线分别于点P₁、P₂,且O为P₁、P₂的中点,

所以P₁与P₂关于原点对称.

若设P₁(x₀,y₀),则P₂(-x₀,-y₀),

所以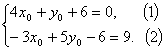

（1）+（2 ）得x₀+6y₀=0.

所以点P₁(x₀,y₀)、P₂(-x₀,-y₀)都满足方程x+6y=0.

因为过两点的直线有且只有一条,且该直线过原点,

所以所求直线l的方程即为y=x.

  绿色通道:与两直线交点有关的直线方程问题,用一般式较其他形式方便,另外注意解析几何中与交点有关的问题,常采用设点而不求点的方法,设而不求是解析几何中常用的方法.