
【题目】已知A={﹣2,3a﹣1,a2﹣3},B={a﹣2,a﹣1,a+1},若A∩B={﹣2},求a的值.
【答案】解:∵A∩B={﹣2},∴﹣2∈B;
∴当a﹣2=﹣2时,a=0,此时A={﹣3,﹣2,﹣1},B={﹣2,﹣1,1},
这样A∩B={﹣2,﹣1}与A∩B={﹣2}矛盾;
当a﹣1=﹣2时,a=﹣1,此时a2﹣1=﹣2,集合A不成立,应舍去;
当a+1=﹣2时,a=﹣3,此时A={﹣2,﹣10,6},B={﹣5,﹣4,﹣2},A∩B={﹣2}满足题意;
∴a=﹣3
【解析】由A∩B={﹣2}得﹣2∈B,分a﹣2=﹣2,a﹣1=﹣2,a+1=﹣2三种情况讨论,要注意元素的互异性.
【考点精析】通过灵活运用集合的交集运算,掌握交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立即可以解答此题.
B,反之也成立即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产100件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为500件,产品销售数量为![]() 件时,销售所得的收入为
件时,销售所得的收入为![]() 万元.
万元.
(1)该公司这种产品的年生产量为![]() 件,生产并销售这种产品所得到的利润关于当年产量
件,生产并销售这种产品所得到的利润关于当年产量![]() 的函数为
的函数为![]() ,求
,求![]() ;
;
(2)当该公司的年产量为多少件时,当年所获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=xlnx-a(x-1)2-x,g(x)=lnx-2a(x-1),其中常数a∈R.
(Ⅰ)讨论g(x)的单调性;
(Ⅱ)当a>0时,若f(x)有两个零点x1,x2(x1<x2),求证:在区间(1,+∞)上存在f(x)的极值点x0,使得x0lnx0+lnx0-2x0>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
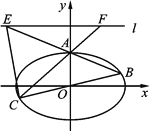
【题目】如图,在平面直角坐标系![]() 中,椭圆:
中,椭圆: ![]() 的离心率为
的离心率为![]() ,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆上的点的距离的最小值为1.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 已知椭圆的上顶点为A,点B,C是上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() .
.
① 求证: ![]() 为定值;
为定值;
② 求△CEF的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com