
【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地![]() 规划建成一个矩形的高科技工业园区.已知
规划建成一个矩形的高科技工业园区.已知![]() ,
,![]() ,
,![]() ,曲线段
,曲线段![]() 是以点
是以点![]() 为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在![]() 、
、![]() 上,且一个顶点
上,且一个顶点![]() 落在曲线段
落在曲线段![]() 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到![]() ).
).

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.

(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.线性回归直线![]() 必经过点
必经过点![]() ,
,![]() ,…
,…![]() 中心点
中心点![]()
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.若两个随机变量的线性相关性越强,则相关系数![]() 的绝对值越接近于1
的绝对值越接近于1
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(![]() 天)内
天)内![]() 天的空气质量指数
天的空气质量指数![]() 的监测数据,结果统计如下:
的监测数据,结果统计如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 |
|
|
|
|
|
|
|
(1)若某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关
)的关
系式为:

试估计在本年内随机抽取一天,该天经济损失![]() 大于
大于![]() 元且不超过
元且不超过![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有![]() 天是在供暖季,其中有
天是在供暖季,其中有![]() 天为重度污染,完成下面
天为重度污染,完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
|
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图所示的频率分布直方图.
,后得到如图所示的频率分布直方图.
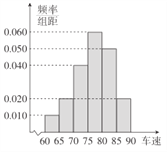
(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?
(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?
(Ⅲ)在抽取的40辆且速度在![]() (km/h)内的汽车中任取2辆,求这2辆车车速都在
(km/h)内的汽车中任取2辆,求这2辆车车速都在![]() (km/h)内的概率.
(km/h)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有奇数条线段,甲乙两人做如下游戏:两人轮流(甲先乙后)给任一条尚未设定方向的线段设定一个方向,直至某次(甲)设定后,所有线段各有了一个方向为止.如果最后得到的所有向量之和的模长不小于原来每条线段长,则甲获胜,否则乙获胜.问:谁有必胜策略?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两支围棋队各5名队员按事先排好的顺序进行擂台赛,双方1号队员先赛,负者被淘汰;然后负方的2号队员再与对方的胜者比赛,负者又被淘汰.依次类推,直到有一方队员全部被淘汰,则宣布另一方获胜.假设每名队员的实力相当,则比赛结束时甲队未上场队员数![]() 的数学期望
的数学期望![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
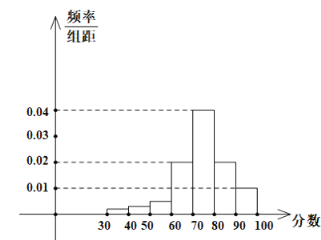
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com