
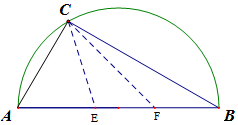
 如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是$∠ECF=\frac{π}{6}$,点E,F在直径AB上,且$∠ABC=\frac{π}{6}$.分析 (1)由已知利用余弦定理,即可求AE的长;
(2)设∠ACE=α,求出CF,CE,利用三角形面积公式可求S△CEF,求出最大值,即可求该空地产生最大经济价值时种植甲种水果的面积.
解答 (本小题满分16分)
解:(1)由已知得△ABC为直角三角形,因为AB=8,$∠ABC=\frac{π}{6}$,
所以$∠BAC=\frac{π}{3}$,AC=4,
在△ACE中,由余弦定理:CE2=AC2+AE2-2AC•AEcosA,且$CE=\sqrt{13}$,
所以13=16+AE2-4AE,
解得AE=1或AE=3,…(4分)
(2)因为$∠ACB=\frac{π}{2}$,$∠ECF=\frac{π}{6}$,
所以∠ACE=α$∈[0,\frac{π}{3}]$,
所以$∠AFC=π-∠A-∠ACF=π-\frac{π}{3}-({α+\frac{π}{6}})=\frac{π}{2}-α$,…(6分)
在△ACF中由正弦定理得:$\frac{CF}{sinA}=\frac{AC}{sin∠CFA}=\frac{AC}{{sin(\frac{π}{2}-α)}}=\frac{AC}{cosα}$,
所以$CF=\frac{{2\sqrt{3}}}{cosα}$,…(8分)
在△ACE中,由正弦定理得:$\frac{CE}{sinA}=\frac{AC}{sin∠AEC}=\frac{AC}{{sin(\frac{π}{3}+α)}}$,
所以$CE=\frac{{2\sqrt{3}}}{{sin(\frac{π}{3}+α)}}$,…(10分)
由于:${S_{△ECF}}=\frac{1}{2}CE•CFsin∠ECF=\frac{3}{{sin(\frac{π}{3}+α)cosα}}=\frac{12}{{2sin(2α+\frac{π}{3})+\sqrt{3}}}$,…(14分)
因为$α∈[0,\frac{π}{3}]$,所以$\frac{π}{3}≤2α+\frac{π}{3}≤π$,所以$0≤sin(2α+\frac{π}{3})≤1$,
所以当$sin(2α+\frac{π}{3})=0$时,S△ECF取最大值为$4\sqrt{3}$.…(16分)
点评 本题主要考查了正弦定理、余弦定理在解三角形中的运用,考查三角形面积的计算,考查了正弦函数的最值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知:平行四边形ABCD,对角线AC,BD交于点O,点E为线段OB中点,完成下列各题(用于填空的向量为图中已有有向线段所表示向量).
已知:平行四边形ABCD,对角线AC,BD交于点O,点E为线段OB中点,完成下列各题(用于填空的向量为图中已有有向线段所表示向量).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{π}{2}})∪[{\frac{2π}{3},π})$ | B. | $[{\frac{2π}{3},π})$ | C. | $[{0,\frac{π}{2}})∪[{\frac{5π}{6},π})$ | D. | $[{\frac{5π}{6},π})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com