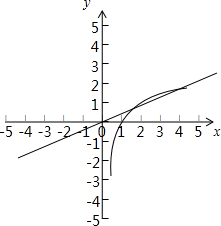Question

设函数f（x）=kx-lnx，x₁、x₂是关于x的方程f（x）=0的两根，且x₁＜x₂，则下列说法正确的是

 

（请将你认为正确的序号都填上）．
①k的取值范围是（-∞，

1

e

）；
②x₁x₂＞e；
③

x2

x1

随k的增大而减小；
④

lnx1

x1-1

＞

lnx2

x2-1

．

Answer 1

考点：利用导数研究函数的单调性

专题：导数的综合应用

分析：根据函数的零点与方程的根的关系，数形结合即可得出结论．

解答： 解：y=kx-lnx的零点，就是kx=lnx的根记f（x）=kx，g（x）=lnx，它们的图象如图所示

当他们有两个公共点时，必有k＞0，且0＜x₁＜x₂．
y'=k-

1

x

其中k＞0，x＞0
可知当0＜x＜

1

k

时，y'＜0，而x＞

1

k

时，y'＞0
所以y=kx-lnx在x=

1

k

处取得极小值y_min=1-ln

1

k

要使得y有两个零点，必有1-ln

1

k

＜0，解得0＜k＜

1

e

，
此时，y有两个零点，于是①错误
当k=

1

e

时，函数y只有一个零点x=e
于是当函数有两个零点时，两个零点必定在e的异侧
即x₁＜e，x₂＞e，而x₁＞1，故x₁x₂＞e，②正确；
当k由小变大时，x₁逐渐增大，而x₂逐渐减小，故

x2

x1

逐渐减小，③正确
记h（x）=

lnx

x-1

=

lnx-ln1

x-1

，表示g（x）=lnx上的动点（x，lnx）与定点（1，0）连线的斜率
由于g（x）=lnx是凸函数，于是h（x）是减函数，④正确
故答案为②③④．

点评：本题是函数与方程的综合问题，主要考查利用导数求函数的极值问题，考查学生数形结合思想的运用能力及运算求解能力，属于难题．