
【题目】已知f(x)=3sinx﹣πx,命题p:x∈(0, ![]() ),f(x)<0,则( )
),f(x)<0,则( )
A.p是假命题,¬p:?x∈(0, ![]() ),f(x)≥0
),f(x)≥0
B.p是假命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
C.p是真命题,¬p:?x∈(0, ![]() ),f(x)>0
),f(x)>0
D.p是真命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.

(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,①![]() 的一个充要条件是
的一个充要条件是![]() 与它的共轭复数相等:
与它的共轭复数相等:
②利用独立性检验来考查两个分类变量![]() ,
,![]() 是否有关系,当随机变量
是否有关系,当随机变量![]() 的观测值
的观测值![]() 值越大,“
值越大,“![]() 与
与![]() 有关系”成立的可能性越大;
有关系”成立的可能性越大;
③在回归分析模型中,若相关指数越大,则残差平方和越小,模型的拟合效果越好;
④若![]() ,
,![]() 是两个相等的实数,则
是两个相等的实数,则![]() 是纯虚数;
是纯虚数;
⑤某校高三共有![]() 个班,
个班,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,由此推测各班都超过
人,由此推测各班都超过![]() 人,这个推理过程是演绎推理.
人,这个推理过程是演绎推理.
其中真命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的![]() 车辆驾驶人员血液、呼气酒精含量阀值与检验
车辆驾驶人员血液、呼气酒精含量阀值与检验![]() 国家标准
国家标准![]() 新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克
新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克![]() 百毫升,小于80毫克
百毫升,小于80毫克![]() 百毫升为饮酒驾车,血液中的酒精含量大于或等于80毫克
百毫升为饮酒驾车,血液中的酒精含量大于或等于80毫克![]() 百毫升为醉酒驾车
百毫升为醉酒驾车![]() 经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如图:
经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如图:

该函数近似模型如下: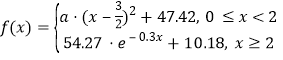 ,又已知刚好过1小时时测得酒精含量值为
,又已知刚好过1小时时测得酒精含量值为![]() 毫克
毫克![]() 百毫升
百毫升![]() 根据上述条件,回答以下问题:
根据上述条件,回答以下问题:
![]() 试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值?最大值是多少?
试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值?最大值是多少?
![]() 试计算喝一瓶啤酒后多少小时后才可以驾车?
试计算喝一瓶啤酒后多少小时后才可以驾车?![]() 时间以整小时计算
时间以整小时计算![]()
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(n)=1+ ![]() +
+ ![]() +…+
+…+ ![]() (n∈N*),计算可得f(2)=
(n∈N*),计算可得f(2)= ![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)> ![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)> ![]() ,推测当n≥2时,有 .
,推测当n≥2时,有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线l:
,直线l:![]() ,设圆C的半径为1,圆心在l上.
,设圆C的半径为1,圆心在l上.
![]() 若圆心C也在直线
若圆心C也在直线![]() 上,过A作圆C的切线,求切线方程;
上,过A作圆C的切线,求切线方程;
![]() 若圆C上存在点M,使
若圆C上存在点M,使![]() ,求圆心C的横坐标a取值范围.
,求圆心C的横坐标a取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
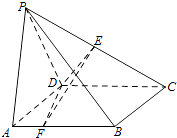
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,AD=PD=2,PA=2 ![]() ,∠PDC=120°,点E为线段PC的中点,点F在线段AB上. (Ⅰ)若AF=
,∠PDC=120°,点E为线段PC的中点,点F在线段AB上. (Ⅰ)若AF= ![]() ,求证:CD⊥EF;
,求证:CD⊥EF;
(Ⅱ)设平面DEF与平面DPA所成二面角的平面角为θ,试确定点F的位置,使得cosθ= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com