[题目]已知极点与直角坐标系原点重合.极轴与x轴的正半轴重合.圆C的极坐标方程为.直线l的参数方程为为参数．若.直线l与x轴的交点为M.N是圆C上一动点.求的最小值,若直线l被圆C截得的弦长等于圆C的半径.求a的值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知极点与直角坐标系原点重合，极轴与x轴的正半轴重合，圆C的极坐标方程为，直线l的参数方程为为参数．

若，直线l与x轴的交点为M，N是圆C上一动点，求的最小值；

若直线l被圆C截得的弦长等于圆C的半径，求a的值．

【答案】（1）；（2）。

【解析】

（1）求出圆C的圆心和半径，M点坐标，则|MN|的最小值为|MC|-r；（2）由垂径定理可知圆心到直线l的距离为半径的倍，列出方程解出．

（1）当时，圆的极坐标方程为，可化为，

化为直角坐标方程为，即.

直线的普通方程为，与轴的交点的坐标为

因为圆心与点的距离为，

所以的最小值为.

（2）由可得，

所以圆的普通方程为

因为直线被圆截得的弦长等于圆的半径，

所以由垂径定理及勾股定理得：圆心到直线的距离为圆半径的倍，

所以.

解得，又，所以

练习册系列答案

一线名师口算应用题天天练一本全系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设函数，（其中，，），在上既无最大值，也无最小值，且，则下列结论成立的是（）

A.若对任意，则

B.的图象关于点中心对称

C.函数的单调减区间为

D.函数的图象相邻两条对称轴之间的距离是

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知为的三个内角，且其对边分别为，若．

（1）求角的值；

（2）若，求的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形.

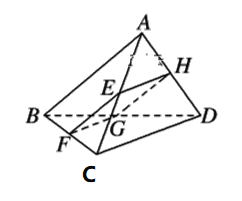
(1)求证：AB∥平面EFGH

(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2019年，我国施行个人所得税专项附加扣除办法，涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有人，现采用分层抽样的方法，从该单位上述员工中抽取人调查专项附加扣除的享受情况.

（Ⅰ）应从老、中、青员工中分别抽取多少人？

（Ⅱ）抽取的25人中，享受至少两项专项附加扣除的员工有6人，分别记为.享受情况如右表，其中“”表示享受，“×”表示不享受.现从这6人中随机抽取2人接受采访.

员工项目	A	B	C	D	E	F
子女教育	○	○	×	○	×	○
继续教育	×	×	○	×	○	○
大病医疗	×	×	×	○	×	×
住房贷款利息	○	○	×	×	○	○
住房租金	×	×	○	×	×	×
赡养老人	○	○	×	×	×	○