
回答下列问题:
(1)
若θ角的终边与α角的终边关于x轴对称,则θ+α________;(2)
若θ角的终边与α角的终边关于y轴对称,则θ+α________;(3)
若θ角的终边与α角的终边关于原点对称,则θ-α________;(4)
若θ角的终边与α角的终边关于直线y=x对称,则θ+α________;(5)
若θ角的终边与α角的终边互相垂直,则θ-α_________;(6)
若θ角的终边上有一点P(a,b),且θ角与α角的终边关于y=-x对称,则α角的终边必过非原点的点Q的坐标是________;(7)
终边落在x轴负半轴的角α的集合为________;(8)
终边在一、三象限的角平分线上的角β的集合是_________.|
解:如图 (1),∵ , , ,(|∠AOC|与|∠BOC|在0°~360°间), ,(|∠AOC|与|∠BOC|在0°~360°间),
∴  ,而∠BOC=-∠AOC. ,而∠BOC=-∠AOC.
∴∠ AOC+∠BOC=0°且 .∴θ+α=k·360°(kÎ
Z). .∴θ+α=k·360°(kÎ
Z).
(2) 如图(2),OA与OB关于y轴对称,设∠AOC与∠BOC在0°~360°间,则 , , , ,
∴  ,而∠AOC=∠BOD,∠BOC+∠BOD=180°. ,而∠AOC=∠BOD,∠BOC+∠BOD=180°.
∴  . .
又∵  , ,
∴ α+θ=(2k+1)180°(kÎ Z).
(3) 是终边一条直线上的两个角,仿照(1)(2)的证明可以得到θ-α=(2k+1)180°(kÎ Z).(4) 仿照(1)、(2)的证明,可以得到α+θ=k·360°+90°(kÎ Z)(5) θ-α=k·360°+90°或θ-α=k·360°-90°(kÎ Z).(6) 如图(3),点Q与点P(a,b)关于直线y=-x对称.
依题意得, Q(-|OB|,|QB|),而|OB|=|OA|=b,|QB|=|PA|=-a,∴点 Q的坐标为(-b,-a).(7){ α|α=180°+k·360°,kÎ Z}={α|α=(2k+1)·180°,kÎ Z}.(8){ β|β=45°+k·180°kÎ Z}.评注:在解题时注意运用数形结合法. |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
①从全年级14个班中任意抽取一个班,再从该班中任意抽取14人,考察他们的学习成绩;②每个班都抽取1人,共计14人,考察这14个学生的成绩;③把学校高三年级的学生按成绩分成优秀、良好、普通三个级别,从中抽取100名学生进行考查(已知若按成绩分,该校高三学生中优秀学生有105名,良好学生有420名,普通学生有175名).根据上面的叙述,试回答下列问题:
(1)上面三种抽取方式中,其总体、个体、样本分别指什么?每一种抽取方式抽取的样本中,其样本容量分别是多少?
(2)上面三种抽取方式各自采用何种抽取样本的方法?
(3)试分别写出上面三种抽取方式各自抽取样本的步骤.
查看答案和解析>>
科目:高中数学 来源:2010年重庆市西南师大附中高三下学期五月月考数学(理) 题型:解答题
(本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n(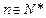 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.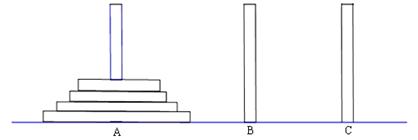
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1) 写出a1,a2,a3,并求出an;
(2) 记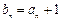 ,求和
,求和 (
( );
);
(其中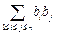 表示所有的积
表示所有的积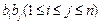 的和)
的和)
(3) 证明: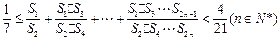 .
.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修1单调性与最大(小)值练习卷(二)(解析版) 题型:填空题
下图表示某市2008年6月份某一天的气温随时间变化的情况,请观察此图回答下列问题:
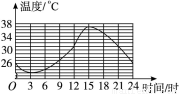
(1)这天的最高气温是__________;
(2)这天共有______个小时的气温在31 ℃以上;
(3)这天在______(时间)范围内温度在上升;
(4)请你预测一下,次日凌晨1点的气温大约在______内.
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省高一第三次月考考试数学 题型:解答题
(12分)如图所示,以AB=4 cm,BC=3 cm的长方形ABCD为底面的长方体被平面斜着截断的几何体,EFGH是它的截面.当AE=5 cm,BF=8 cm,CG=12 cm时,试回答下列问题:
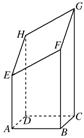
(1)求DH的长;
(2)求这个几何体的体积;
(3)截面四边形EFGH是什么图形?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010年重庆市高三下学期五月月考数学(理) 题型:解答题
1. (本小题满分12分)
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有n( )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.

现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数,回答下列问题:
(1) 写出a1,a2,a3,并求出an;
(2) 记 ,求和
,求和 (
( );
);
(其中 表示所有的积
表示所有的积 的和)
的和)
(3) 证明: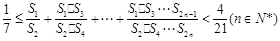 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com