
 把函数
把函数 的图象按向量
的图象按向量 平移,所得曲线的一部分如图所示,则ω、ϕ的值分别是( )
平移,所得曲线的一部分如图所示,则ω、ϕ的值分别是( )



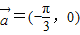 平移,
平移,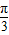 )+φ]的图象,这个函数的图象即为所给的函数的图象,
)+φ]的图象,这个函数的图象即为所给的函数的图象,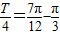 =
=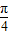
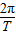 =
=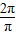 =2
=2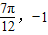 )
)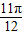 +φ)
+φ)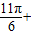 φ=2kπ-
φ=2kπ-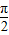 ,k∈z
,k∈z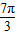 ,k∈z
,k∈z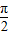
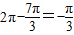


科目:高中数学 来源: 题型:
(本小题满12分.)已知函数![]() .
.
(Ⅰ)当![]() 时,若
时,若![]() ,求函数
,求函数![]() 的值;
的值;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(Ⅲ)把函数![]() 的图象按向量
的图象按向量![]() 平移得到函数
平移得到函数![]() 的图象,若函数
的图象,若函数![]() 是偶函数,写出
是偶函数,写出![]() 最小的向量
最小的向量![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
把函数 的图象按向量
的图象按向量 平移得到函数
平移得到函数 的图象.
的图象.
(1)求函数 的解析式; (2)若
的解析式; (2)若 ,证明:
,证明: .
.
【解析】本试题主要考查了函数 平抑变换和运用函数思想证明不等式。第一问中,利用设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 ,便可以得到结论。第二问中,令
,便可以得到结论。第二问中,令 ,然后求导,利用最小值大于零得到。
,然后求导,利用最小值大于零得到。
(1)解:设 上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入
上任意一点为(x,y)则平移前对应点是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 证明:令 ,……6分
,……6分
则 ……8分
……8分
 ,∴
,∴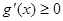 ,∴
,∴ 在
在 上单调递增.……10分
上单调递增.……10分
故 ,即
,即
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省绵阳市高三第二次月考文科数学试卷 题型:选择题
把函数 的图象按向量
的图象按向量 平移后得到函数
平移后得到函数 的图象,则函数
的图象,则函数 在区间
在区间 上的最大值为
上的最大值为
A、1 B、0 C、 D、-1
D、-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com