
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】2017年10月9日,教育部考试中心下发了《关于![]() 年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了
年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了![]() 位市民进行了解,发现支持开展的占
位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民
,在抽取的男性市民![]() 人中支持态度的为
人中支持态度的为![]() 人.
人.
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
(1)完成![]() 列联表
列联表
(2)判断是否有![]() 的把握认为性别与支持有关?
的把握认为性别与支持有关?
附:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率
的离心率![]() .
.
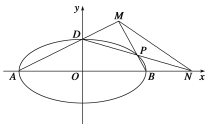
(1)求椭圆![]() 的方程;
的方程;
(2)如图所示,A、B、D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明:2m-k为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(﹣x)=f(x),且当x<0,f(x)=3x+1,若a= ![]() ,b=
,b= ![]() ,c=2
,c=2 ![]() ,则有( )
,则有( )
A.f(a)<f(b)<f(c)
B.f(b)<f(c)<f(a)
C.f(b)<f(a)<f(c)
D.f(c)<f(a)<f(b)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>0,b>0)的离心率为
(a>0,b>0)的离心率为 ![]() ,点A(0,﹣2)与椭圆右焦点F的连线的斜率为
,点A(0,﹣2)与椭圆右焦点F的连线的斜率为 ![]() .
.
(1)求椭圆C的方程;
(2)O为坐标原点,过点A的直线l与椭圆C相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为( ) 
A.20
B.61
C.183
D.548
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线l的参数方程为  (t为参数),在极坐标系(与直角坐标系xoy取相同的单位长度,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2
(t为参数),在极坐标系(与直角坐标系xoy取相同的单位长度,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2 ![]() sinθ.
sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于A,B两点,若点P坐标为(3, ![]() ),求|PA|+|PB|.
),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
①“若x2+y2≠0,则x,y不全为零”的否命题 ②“正多边形都相似”的逆命题
③“若m>0,则x2+x-m=0有实根”的逆否命题④“若x-![]() 是有理数,则x是
是有理数,则x是
无理数”的逆否命题
A、①②③④ B、①③④ C、②③④ D、①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com