
设函数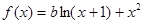
 (提示 :
(提示 :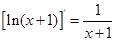 )
)
(1)若函数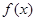 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数 的取值范围;
的取值范围;
(2) 若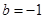 ,证明对任意的正整数n,不等式
,证明对任意的正整数n,不等式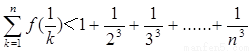 都成立.
都成立.
(1)∵ .
.
又函数f(x)在定义域上是单调函数 ∴f/ (x) ≥0或f/(x)≤0在( - 1,+ ∞)上恒成立.
若f/ (x) ≥0,∵x + 1>0,∴2x2 +2x+b≥0在( - 1,+ ∞)上恒成立.
即b≥-2x2 -2x = 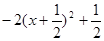 恒成立,由此得b≥
恒成立,由此得b≥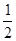 .
.
若f/ (x) ≤0, ∵x + 1>0, ∴2x2 +2x+b≤0,即b≤-(2x2+2x)恒成立,
因-(2x2+2x) 在( - 1,+ ∞)上没有最小值.
∴不存在实数b使f(x) ≤0恒成立.
综上所述,实数b的取值范围是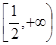 .
.
(2)当b= - 1时,函数f(x) = x2 - ln(x+1)
令函数h(x)=f(x) – x3 = x2 – ln(x+1) – x3.
则h/(x) = -
3x2 +2x - 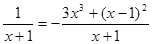 .
.
∴当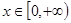 时,h/(x)<0所以函数h(x)在
时,h/(x)<0所以函数h(x)在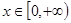 上是单调递减. -------10分
上是单调递减. -------10分
又h(0)=0,∴当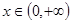 时,恒有h(x) <h(0)=0,
时,恒有h(x) <h(0)=0,
即x2 –
ln(x+1) <x3恒成立.故当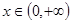 时,有f(x)
<x3.
时,有f(x)
<x3.
∵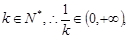 取
取 则有
则有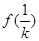 <
<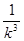 .
.
【解析】略


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2013届山东省济宁市高二3月月考文科数学试卷 题型:解答题
设函数
 (提示 :
(提示 : )
)
(1)若函数 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数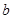 的取值范围;
的取值范围;
(2) 若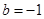 ,证明对任意的正整数n,不等式
,证明对任意的正整数n,不等式 都成立.
都成立.
查看答案和解析>>
科目:高中数学 来源:2010年福建省泉州市南安市鹏峰中学高考数学模拟试卷1(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com