已知以A点为圆心的圆与直线${l 1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切．过点B的动直线l与圆A相交于M.N两点.Q是MN的中点.直线l与l1相交于点P．(1)求圆A的方程,(2)当$|{MN}|=2\sqrt{19}$时.求直线l的方程,(3)求证:$\overrightarrow{BP}•\overrightarrow{BQ}=-5$� 题目和参考答案——青夏教育精英家教网—

10．

已知以A（-1，2）点为圆心的圆与直线${l_1}：\frac{1}{2}x+y+\frac{7}{2}=0$相切．过点B（-2，0）的动直线l与圆A相交于M，N两点，Q是MN的中点，直线l与l₁相交于点P．
（1）求圆A的方程；
（2）当$|{MN}|=2\sqrt{19}$时，求直线l的方程；
（3）求证：$\overrightarrow{BP}•\overrightarrow{BQ}=-5$．

分析（1）设出圆A的半径，根据以点A（-1，2）为圆心的圆与直线l₁：x+2y+7=0相切．点到直线的距离等于半径，我们可以求出圆的半径，进而得到圆的方程；
（2）根据半弦长，弦心距，圆半径构成直角三角形，满足勾股定理，我们可以结合直线l过点B（-2，0），求出直线的斜率，进而得到直线l的方程；
（3）由直线l过点B（-2，0），我们可分直线的斜率存在和不存在两种情况，运用向量的坐标和数量积的坐标表示，综合讨论结果，即可得到结论．

解答解：（1）设圆A的半径为R，由于圆A与直线l₁：x+2y+7=0相切，
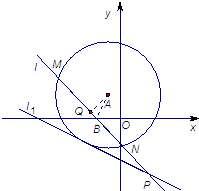
∴R=$\frac{|-1+4+7|}{\sqrt{5}}$=2$\sqrt{5}$，
∴圆A的方程为（x+1）²+（y-2）²=20；
（2）①当直线l与x轴垂直时，易知x=-2符合题意；
②当直线l与x轴不垂直时，
设直线l的方程为y=k（x+2），即kx-y+2k=0，
连接AQ，则AQ⊥MN
∵$|{MN}|=2\sqrt{19}$，∴|AQ|=$\sqrt{20-19}$=1，
则由|AQ|=$\frac{|k-2|}{\sqrt{1+{k}^{2}}}$=1，得k=$\frac{3}{4}$，∴直线l：3x-4y+6=0．
故直线l的方程为x=-2或3x-4y+6=0；
（3）证明：∵AQ⊥BP，∴$\overrightarrow{BQ}$•$\overrightarrow{BP}$=（$\overrightarrow{BA}$+$\overrightarrow{AQ}$）•$\overrightarrow{BP}$=$\overrightarrow{BA}$•$\overrightarrow{BP}$+$\overrightarrow{AQ}$•$\overrightarrow{BP}$=$\overrightarrow{BA}$•$\overrightarrow{BP}$，
①当l与x轴垂直时，易得P（-2，-$\frac{5}{2}$），则$\overrightarrow{BP}$=（0，-$\frac{5}{2}$），又$\overrightarrow{BA}$=（1，2），
∴$\overrightarrow{BQ}$•$\overrightarrow{BP}$=$\overrightarrow{BA}$•$\overrightarrow{BP}$=0×1-$\frac{5}{2}$×2=-5；
②当l的斜率存在时，设直线l的方程为y=k（x+2），
则由$\left\{\begin{array}{l}{y=k（x+2）}\\{x+2y+7=0}\end{array}\right.$，得P（$\frac{-4k-7}{1+2k}$，$\frac{-5k}{1+2k}$），
则$\overrightarrow{BP}$=（$\frac{-5}{1+2k}$，$\frac{-5k}{1+2k}$），
∴$\overrightarrow{BQ}$•$\overrightarrow{BP}$=$\overrightarrow{BA}$•$\overrightarrow{BP}$=$\frac{-5}{1+2k}$+$\frac{-10k}{1+2k}$=-5．
综上所述，$\overrightarrow{BP}•\overrightarrow{BQ}=-5$．

点评本题考查的知识点是直线和圆的方程的应用，直线的一般式方程，圆的标准方程，其中（1）的关键是求出圆的半径，（2）的关键是根据半弦长，弦心距，圆半径构成直角三角形，满足勾股定理，求出弦心距（即圆心到直线的距离），（3）中要注意讨论斜率不存在的情况，这也是解答直线过定点类问题的易忽略点．

练习册系列答案

书屯文化期末寒假期末冲刺假期作业云南人民出版社系列答案

硕源教育中考总复习名师解密系列答案

初中学业水平测试用书激活中考系列答案

赢在寒假期末闯关合肥工业大学出版社系列答案

快乐寒假山西教育出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

20．给定四组数据：甲：1，2，3，4，5；乙：1，3，5，7，9；丙：1，2，3；丁：1，3，5．其中方差最小的一组是（　　）

A．

甲

B．

乙

C．

丙

D．

丁

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

1．已知抛物线${C_1}：{y^2}=8x$的焦点为F，P是抛物线C₁上位于第一象限内的点，|PF|=4，P到双曲线${C_2}：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0\;\;，\;\;b＞0}）$的一条渐近线的距离为2，则双曲线C₂的离心率为$\frac{5}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．在等差数列{a_n}中，d＞0，若a₁+a₄+a₇=12，a₁a₄a₇=28，数列{b_n}是等比数列，b₁=16，a₂b₂=4．
（1）求{a_n}和{b_n}的通项公式；
（2）令${c_n}={a_n}•{b_n}（n∈{N^*}）$，求{c_n}的前n项和T_n．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．在平面直角坐标系中，已知点M（1，0），P（x，y）为平面上一动点，P到直线x=2的距离为d，$\frac{|PM|}{d}$=$\frac{\sqrt{2}}{2}$．
（Ⅰ）求点P的轨迹C的方程；
（Ⅱ）不过原点O的直线l与C相交于A，B两点，线段AB的中点为D，直线OD与直线x=2交点的纵坐标为1，求△OAB面积的最大值及此时直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．已知两个正数a，b满足3a+2b=1，则$\frac{3}{a}$+$\frac{2}{b}$的最小值是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．已知平面上动点M到直线y=-2的距离比它到点F（0，1）的距离多1．
（Ⅰ）求动点M的轨迹方程；
（Ⅱ）设动点M形成的曲线为E，过点P（0，-1）的直线l交曲线E于A，B两点，若直线OA和直线OB的斜率之和为2（其中O为坐标原点），求直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题