
【题目】某闯关游戏规划是:先后掷两枚骰子,将此试验重复![]() 轮,第
轮,第![]() 轮的点数分别记为
轮的点数分别记为![]() ,如果点数满足
,如果点数满足![]() ,则认为第
,则认为第![]() 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(1)求第1轮闯关成功的概率;
(2)如果第![]() 轮闯关成功所获的奖金(单位:元)
轮闯关成功所获的奖金(单位:元) ![]() ,求某人闯关获得奖金不超过2500元的概率;
,求某人闯关获得奖金不超过2500元的概率;
(3)如果游戏只进行到第4轮,第4轮后无论游戏成功与否,都终止游戏,记进行的轮数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)枚举法列出所有满足条件的数对![]() 即可;
即可;
(2)由![]() ,得
,得![]() ,由(1)每轮过关的概率为
,由(1)每轮过关的概率为![]() ,某人闯关获得奖金不超过2500元的概率:
,某人闯关获得奖金不超过2500元的概率:![]() ;
;
(3)设游戏第![]() 轮后终止的概率为
轮后终止的概率为![]() ,分别求出相应的概率,由此能求出X的分布列和数学期望.
,分别求出相应的概率,由此能求出X的分布列和数学期望.
解:(1)若第1轮闯关成功,
当![]() 时,
时, ![]() ,因此
,因此![]() ;
;
当![]() 时,
时, ![]() ,因此
,因此![]() ;
;
当![]() 时,
时,![]() ,因此
,因此![]() ;
;
当![]() 时,
时,![]() ,因此
,因此![]() ;
;
当![]() 时,
时, ![]() ,因此
,因此![]() ;
;
当![]() 时,
时, ![]() ,因此
,因此![]() 无值.
无值.
记“第1轮闯关成功”为事件![]() ,
,
则第1轮闯关成功的概率![]() .
.
(2)由![]() ,得
,得![]() ,
,
由(1)知每轮闯关成功的概率为![]() .
.
某人闯关获得奖金不超过2500元的概率![]()
![]() .
.
(3)依题意![]() 的所有可能取值为1,2,3,4,
的所有可能取值为1,2,3,4,
设游戏第![]() 轮后终止的概率为
轮后终止的概率为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
![]() .
.
故![]() 的分布列为
的分布列为
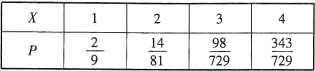
因此数学期望![]()
![]() .
.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 在该直角坐标系下的普通方程;
在该直角坐标系下的普通方程;
(2)动点![]() 在曲线
在曲线![]() 上,动点
上,动点![]() 在直线
在直线![]() 上,定点
上,定点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )与双曲线
)与双曲线![]() (
(![]() ,
,![]() )有相同的焦点
)有相同的焦点![]() ,点
,点![]() 是两条曲线的一个交点,且
是两条曲线的一个交点,且![]() 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:

①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2016年6月30天的空气质量指数如下:
35 | 54 | 80 | 86 | 72 | 85 | 58 | 125 | 111 | 53 |
10 | 66 | 46 | 36 | 18 | 25 | 23 | 40 | 60 | 89 |
88 | 54 | 79 | 14 | 16 | 40 | 59 | 67 | 111 | 62 |
你觉得这个月的空气质量如何?请设计适当的频率分布直方图展示这组数据,并结合空气质量分级标准分析数据.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,且曲线
轴的正半轴为极轴建立极坐标系,且曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 的斜率为
的斜率为![]() ,判断直线
,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)求![]() 与
与![]() 交点的极坐标(
交点的极坐标(![]() ,
,![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com