练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知是给定的平面，设不在内的任意两点M，N所在的直线为l，则下列命题正确的是（ ）

    A.在内存在直线与直线l异面

    B.在内存在直线与直线l相交

    C.在内存在直线与直线l平行

    D.存在过直线l的平面与平行

    【答案】A

    【解析】

    利用M、N是不在内的任意两点，可得直线l与平面平行或相交，进而可判断直线与平面内直线的位置关系.

    M、N是不在内的任意两点，则直线l与平面平行或相交，

    若l与平面平行，则在内不存在直线与直线l相交，所以B错误：

    若直线l与平面相交，则不存在过直线l的平面与平行，所以D错误：

    若直线l与平面相交，则在内都不存在直线与直线l平行，所以C错误；

    不论直线l与平面平行还是相交.在内都存在直线与直线l异面，所以A正确.

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了判断英语词汇量与阅读水平是否相互独立，某语言培训机构随机抽取了100位英语学习者进行调查，经过计算的观测值为7，根据这一数据分析，下列说法正确的是（ ）

    附：

    0.050

    0.010

    0.005

    0.001

    3.841

    6.635

    7.879

    10.828

    A.有99%以上的把握认为英语词汇量与阅读水平无关

    B.有99.5%以上的把握认为英语词汇量与阅读水平有关

    C.有99.9%以上的把握认为英语词汇量与阅读水平有关

    D.在犯错误的概率不超过1%的前提下，可以认为英语词汇量与阅读水平有关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】每年的台风都对泉州地区的渔业造成较大的经济损失．某保险公司为此开发了针对渔船的险种，并将投保的渔船分为I，II两类，两类渔船的比例如图所示．经统计，2019年I，II两类渔船的台风遭损率分别为和．2020年初，在修复遭损船只的基础上，对I类渔船中的进一步改造．保险公司预估这些经过改造的渔船2020年的台风遭损率将降为，而其他渔船的台风遭损率不变．假设投保的渔船不变，则下列叙述中正确的是（ ）

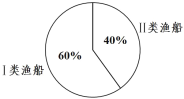
    A.2019年投保的渔船的台风遭损率为

    B.2019年所有因台风遭损的投保的渔船中，I类渔船所占的比例不超过

    C.预估2020年I类渔船的台风遭损率会小于II类渔船的台风遭损率的两倍

    D.预估2020年经过进一步改造的渔船因台风遭损的数量少于II类渔船因台风遭损的数量

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（，为自然对数的底数）.

    （1）若函数在点处的切线的斜率为，求实数的值；

    （2）当时，讨论函数的单调性；

    （3）若关于的不等式在区间上恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是给定的平面，设不在内的任意两点M，N所在的直线为l，则下列命题正确的是（ ）

    A.在内存在直线与直线l异面

    B.在内存在直线与直线l相交

    C.在内存在直线与直线l平行

    D.存在过直线l的平面与平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】上世纪末河南出土的以鹤的尺骨（翅骨）制成的“骨笛”（图1），充分展示了我国古代高超的音律艺术及先进的数学水平，也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春（秋）分”，“夏（冬）至”的示意图，图3是某骨笛的部分测量数据（骨笛的弯曲忽略不计），夏至（或冬至）日光（当日正午太阳光线）与春秋分日光（当日正午太阳光线）的夹角等于黄赤交角.

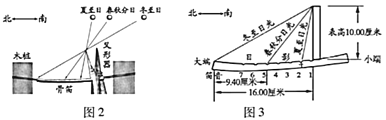
    由历法理论知，黄赤交角近1万年持续减小，其正切值及对应的年代如下表：

    黄赤交角

    正切值

    0.439

    0.444

    0.450

    0.455

    0.461

    年代

    公元元年

    公元前2000年

    公元前4000年

    公元前6000年

    公元前8000年

    根据以上信息，通过计算黄赤交角，可估计该骨笛的大致年代是( )

    A.公元前2000年到公元元年B.公元前4000年到公元前2000年

    C.公元前6000年到公元前4000年D.早于公元前6000年

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体ABCD﹣A1B1C1D1中，AA1＝8，AB＝3，AD＝8，点M是棱AD的中点，点N是棱AA1的中点，P是侧面四边形ADD1A1内一动点（含边界），若C1P∥平面CMN，则线段C1P长度的取值范围是（　　）

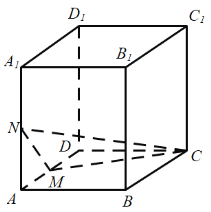
    A.B.[4，5]C.[3，5]D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面直角坐标系中，曲线的方程为，以原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为．若将曲线上的所有点的横坐标缩小到原来的一半，纵坐标伸长到原来的倍，得曲线．

    （1）写出直线和曲线的直角坐标方程；

    （2）设点， 直线与曲线的两个交点分别为，，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两位同学参加某个知识答题游戏节目，答题分两轮，第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”，答题规则是：每位同学各自从备选的5道不同题中随机抽出3道题进行答题，答对一题加10分，答错一题（不答视为答错）减5分，已知甲能答对备选5道题中的每道题的概率都是，乙恰能答对备选5道题中的其中3道题；第一轮答题完毕后进行第二轮“轮流坐庄答题环节”，答题规则是：先确定一人坐庄答题，若答对，继续答下一题…，直到答错，则换人（换庄）答下一题…以此类推.例如若甲首先坐庄，则他答第1题，若答对继续答第2题，如果第2题也答对，继续答第3题，直到他答错则换成乙坐庄开始答下一题，…直到乙答错再换成甲坐庄答题，依次类推两人共计答完20道题游戏结束，假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答，且记第道题也由该同学（最先答题的同学）作答的概率为（），其中，已知供甲乙回答的20道题中，甲，乙两人答对其中每道题的概率都是，如果某位同学有机会答第道题且回答正确则该同学加10分，答错（不答视为答错）则减5分，甲乙答题相互独立；两轮答题完毕总得分高者胜出.回答下列问题

    （1）请预测第二轮最先开始作答的是谁？并说明理由

    （2）①求第二轮答题中，；

    ②求证为等比数列，并求（）的表达式.

    查看答案和解析>>

    同步练习册答案