
【题目】如果无穷数列{an}的所有项恰好构成全体正整数的一个排列,则称数列{an}具有性质P.
(Ⅰ)若an![]() (k∈N*),判断数列{an}是否具有性质P,并说明理由,
(k∈N*),判断数列{an}是否具有性质P,并说明理由,
(Ⅱ)若数列{an}具有性质P,求证:{an}中一定存在三项ai,aj,ak(i<j<k)构成公差为奇数的等差数列;
(Ⅲ)若数列{an}具有性质P,则{an}中是否一定存在四项ai,aj,ak,al,(i<j<k<l)构成公差为奇数的等差数列?证明你的结论.
【答案】(Ⅰ)数列{an}具有性质P.见解析(Ⅱ)见解析(Ⅲ)不一定存在,见解析
【解析】
(Ⅰ)分n为奇数,n为偶数讨论,研究an包含的数的情况,即得解;
(Ⅱ)考虑![]() ,令
,令![]() ,从
,从![]() 开始寻找第一个大于M的项,记为:
开始寻找第一个大于M的项,记为:![]() ,分
,分![]() 为奇数,偶数讨论,分别构造
为奇数,偶数讨论,分别构造![]() ,
,![]() 为公差为奇数的等差数列,即得证.
为公差为奇数的等差数列,即得证.
(Ⅲ)构造反例:![]() 为1,2,4,3,6,8,…,2k-1,4k-2,4k,…,利用反证法,即得证,
为1,2,4,3,6,8,…,2k-1,4k-2,4k,…,利用反证法,即得证,
(Ⅰ)解:∵an![]() (k∈N*),∴数列{an}具有性质P.
(k∈N*),∴数列{an}具有性质P.
理由如下:
当n为奇数,n∈N*时,an=n+1包含所有的正偶数,
当n为偶数,n∈N*时,an=n﹣1包含所有的正奇数,
∴无穷数列{an}的所有项恰好构成全体正整数的一个排列,
∴数列{an}具有性质P.
(Ⅱ)证明:不妨设![]()
考虑![]() ,令
,令![]() ,
,
从![]() 开始寻找第一个大于M的项,记为:
开始寻找第一个大于M的项,记为:![]() ,则
,则![]() 中含有1,2,且
中含有1,2,且![]() 为前j项中的最大项(
为前j项中的最大项(![]() )
)
(i)若![]() 为奇数,
为奇数,![]() ,所以
,所以![]() 在
在![]() 之后,记为
之后,记为![]() ,则
,则![]() ,
,![]() 为公差为奇数的等差数列;
为公差为奇数的等差数列;
(ii) 若![]() 为偶数,令
为偶数,令![]() ,则
,则![]() ,
,![]() 为公差为奇数的等差数列.
为公差为奇数的等差数列.
故结论成立.
(Ⅲ)不一定存在
例如![]() 为1,2,4,3,6,8,…,2k-1,4k-2,4k,…,
为1,2,4,3,6,8,…,2k-1,4k-2,4k,…,
即每三项构成一组,第k组的通项公式为:2k-1,4k-2,4k,
假设存在4项构成公差为奇数的等差数列,则存在三项(偶数,奇数,偶数)成等差,
由于![]() 中,任意一项奇数
中,任意一项奇数![]() 后面的偶数都大于等于2
后面的偶数都大于等于2![]() ,
,
因此不可能存在三项(偶数,奇数,偶数)成等差.
故假设不成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
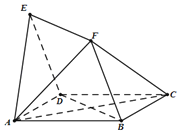
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知{an}是等差数列,其前n项和Sn=n2﹣2n+b﹣1,{bn}是等比数列,其前n项和Tn![]() ,则数列{ bn +an}的前5项和为( )
,则数列{ bn +an}的前5项和为( )
A.37B.-27C.77D.46
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年北京市百项疏堵工程基本完成.有关部门为了解疏堵工程完成前后早高峰时段公交车运行情况,调取某路公交车早高峰时段全程所用时间(单位:分钟)的数据,从疏堵工程完成前的数据中随机抽取5个数据,记为A组,从疏堵工程完成后的数据中随机抽取5个数据,记为B组.
A组:128,100,151,125,120
B组:100,102,96,101,![]()
己知B组数据的中位数为100,且从中随机抽取一个数不小于100的概率是![]() .
.
(1)求a的值;
(2)该路公交车全程所用时间不超过100分钟,称为“正点运行”从A,B两组数据中各随机抽取一个数据,记两次运行中正点运行的次数为X,求X的分布列及期望;
(3)试比较A,B两组数据方差的大小(不要求计算),并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com