练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列有关命题的说法正确的是（ ）

    A. 命题“若，则”的否命题为：“若则”

    B. 若为真命题，为假命题，则均为假命题

    C. 命题“若成等比数列，则”的逆命题为真命题

    D. 命题“若，则”的逆否命题为真命题

    【答案】D

    【解析】

    分别写出命题的否命题，可判定A不正确；根据复合命题的真假判定，可判定B不正确；根据等比数列的定义，即可判定C不正确；根据四种命题的关系，可判定D正确，得到答案.

    对于A中，命题“若，则”的否命题为：“若则”，所以不正确；

    对于B中，由为真命题，为假命题，则为真命题，均为假命题，所以不正确；

    对于C中，命题“若成等比数列，则”的逆命题为“若，则成等比数列”为假命题，所以不正确；

    对于D中，命题“若，则”为真命题，所以命题的逆否命题也是真命题，故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为）作为样本（样本容量为）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图,已知得分在[50，60），[90，100]的频数分别为8，2.

    （1）求样本容量和频率分布直方图中的的值；

    （2）估计本次竞赛学生成绩的中位数；

    （3）在选取的样本中，从竞赛成绩在分以上（含分）的学生中随机抽取名学生，求所抽取的名学生中至少有一人得分在内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）若对任意，且，都有，求实数的取值范围；

    （2）在第（1）问求出的实数的范围内，若存在一个与有关的负数，使得对任意时恒成立，求的最小值及相应的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某电商2019年12月1日至12月16日的日销售量（单位：件）统计图，销量小于100称为该商品滞销，销量大于200称为该商品畅销，则下列关于该商品在这16天的销量的说法不正确的是( )

    A.该商品出现过连续4天畅销

    B.该商品畅销的频率为0.5

    C.相邻两天该商品销量之差的最大值为195

    D.该商品销量的平均数小于200

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大提出，坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村真脱贫，坚持扶贫同扶智相结合，帮助贫困村种植蜜柚，并利用电商进行销售，为了更好地销售，现从该村的蜜柚树上随机摘下了100个蜜柚进行测重，其质量分别在， ， ， ， ， （单位：克）中，其频率分布直方图如图所示.

    （1）按分层抽样的方法从质量落在， 的蜜柚中抽取5个，再从这5个蜜柚中随机抽取2个，求这2个蜜柚质量均小于2000克的概率；

    （2）以各组数据的中间数代表这组数据的平均水平，以频率代表概率，已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售，某电商提出两种收购方案：

    A.所有蜜柚均以40元/千克收购；

    B．低于2250克的蜜柚以60元/个收购，高于或等于2250克的以80元/个收购.

    请你通过计算为该村选择收益最好的方案.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆

    （1）求圆关于直线对称的圆的标准方程；

    （2）过点的直线被圆截得的弦长为8，求直线的方程；

    （3）当取何值时，直线与圆相交的弦长最短，并求出最短弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】连结圆周上九个不同点的36条弦要么染成红色，要么染成蓝色，我们称它们为“红边”或“蓝边”.假定由这九个点中每三个点为顶点的三角形中都含有“红边”.证明：这九个点中存在四个点，两两连结的六条边都是红边.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为自然底数），且.

    (1)当时，对任意的，都有不等式，求实数的取值范围；

    (2)若函数是上的减函数，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体，关于其结构特征，下列说法不正确的是

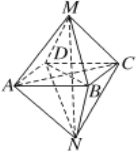
    A. 该几何体是由两个同底的四棱锥组成的几何体

    B. 该几何体有12条棱、6个顶点

    C. 该几何体有8个面，并且各面均为三角形

    D. 该几何体有9个面，其中一个面是四边形，其余均为三角形

    查看答案和解析>>

    同步练习册答案