
【题目】(1)已知直线l过点![]() ,它的一个方向向量为
,它的一个方向向量为![]() .
.
①求直线l的方程;
②一组直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 都与直线l平行,它们到直线l的距离依次为d,
都与直线l平行,它们到直线l的距离依次为d,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),且直线
),且直线![]() 恰好经过原点,试用n表示d的关系式,并求出直线
恰好经过原点,试用n表示d的关系式,并求出直线![]() 的方程(用n、i表示);
的方程(用n、i表示);
(2)在坐标平面上,是否存在一个含有无穷多条直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的直线簇,使它同时满足以下三个条件:①点
的直线簇,使它同时满足以下三个条件:①点![]() ;②
;②![]() ,其中
,其中![]() 是直线
是直线![]() 的斜率,
的斜率,![]() 和
和![]() 分别为直线
分别为直线![]() 在x轴和y轴上的截距;③
在x轴和y轴上的截距;③![]()
![]() .
.
【答案】(1)①![]() ;②
;②![]() ,
,![]() ;(2)不存在.
;(2)不存在.
【解析】
(1)根据直线的方向向量可得直线的斜率,结合点斜式即可求得直线方程;根据直线平行且过原点,可得直线![]() 的方程,由平行线间距离公式可得n与d的关系式,设出直线
的方程,由平行线间距离公式可得n与d的关系式,设出直线![]() 的方程,根据点到直线距离公式可求得直线方程.
的方程,根据点到直线距离公式可求得直线方程.
(2)假设存在这样的直线簇.先求得![]() ,
,![]() 的表达式,进而表示出
的表达式,进而表示出![]() .通过迭加法求得
.通过迭加法求得![]() ,即可证明当
,即可证明当![]() 时,
时,![]() 与
与![]() 不能成立.
不能成立.
(1)①直线l方向向量为![]()
所以直线的斜率为![]()
直线l过点![]() ,由点斜式方程可得
,由点斜式方程可得
![]()
即直线l的方程为:![]() ;
;
②直线![]() 且经过原点,
且经过原点,
![]() 直线
直线![]() 的方程为:
的方程为:![]()
由题意知直线![]() 到l的距离为
到l的距离为![]() ,根据平行线间距离公式可得
,根据平行线间距离公式可得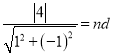
则![]()
设直线![]() 的方程为:
的方程为:![]()
由题意知:直线![]() 到直线l的距离为
到直线l的距离为![]() ,
,
![]()
所以直线![]() 的方程为:
的方程为:![]() ;
;
(2)假设存在满足题意的直线簇.由①知![]() 的方程为:
的方程为:![]() ,
,![]() ,
,
分别令![]() ,
,![]() 得
得![]() ,
,![]() ,
,
由![]() ,即
,即![]() ,
,![]() ,
,
迭加得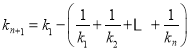 .
.
由③知所有的![]() 同号,仅讨论
同号,仅讨论![]() 的情形,
的情形,
由![]() ,
,
所以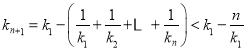
显然,当![]() 时,
时,![]() 与
与![]() 矛盾!
矛盾!
故满足题意的直线簇不存在.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABC,则二面角D﹣AF﹣B的平面角余弦值的取值范围是_____.
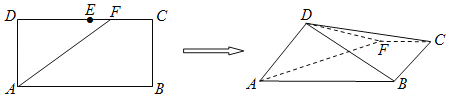
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为迎接端午节,推出两款粽子:花生粽和肉粽.为调查这两款粽子的受欢迎程度,店员连续10天记录了这两种粽子的销售量,如下表表示(其中销售单位:个)
天数 销售量
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
花生粽 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 | 100 |
肉粽 | 88 | 97 | 98 | 95 | 101 | 98 | 103 | 106 | 103 | 111 | 100 |
(1)根据两组数据完成下面茎叶图:
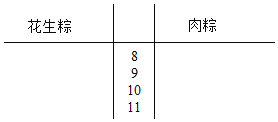
(2)统计学知识,请评述哪款粽子更受欢迎;
(3)求肉粽销售量y关于天数t的线性回归方程,并预估第15天肉粽的销售量(回归方程系数精确到0.1)
参考数据:![]() ,参考公式:
,参考公式: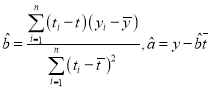
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
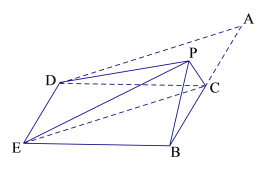
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() .
.

(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是
(1)命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l为直线,![]() ,
,![]() 为两个不同的平面,若
为两个不同的平面,若![]() ,
,![]() ,则
,则![]() ;
;
(3)给定命题p,q,若“![]() 为真命题”,则
为真命题”,则![]() 是假命题;
是假命题;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式![]() 表示的平面区别为
表示的平面区别为![]() .区域
.区域![]() 内的动点
内的动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离之积为2.记点
的距离之积为2.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .过点
.过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 轴,
轴,![]() 为曲线
为曲线![]() 上一点,求
上一点,求![]() 的取值范围;
的取值范围;
(3)若以线段![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com