
【题目】【2017唐山三模】已知函数![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 在区间
在区间![]() 有唯一零点
有唯一零点![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)求导得![]() , 分
, 分![]() ,
, ![]() ,
, ![]() ,三种情况讨论可得单调区间.
,三种情况讨论可得单调区间.
(Ⅱ)由(1)及![]() 可知:仅当极大值等于零,即
可知:仅当极大值等于零,即![]() 且
且 ![]()
所以![]() ,且
,且![]() ,消去
,消去![]() 得
得![]() ,构造函数,证明单调且零点存在且唯一即可.
,构造函数,证明单调且零点存在且唯一即可.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
若![]() ,即
,即![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
若![]() ,即
,即![]() ,则
,则![]() ,仅当
,仅当![]() 时,等号成立,
时,等号成立,
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
若![]() ,即
,即![]() ,则
,则![]() 有两个零点
有两个零点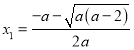 ,
, 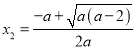 ,
,
由![]() ,
, ![]() 得
得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增.
单调递增.
综上所述,
当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在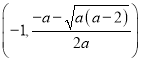 和
和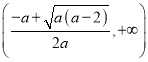 上单调递增,
上单调递增,
在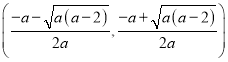 上单调递减.
上单调递减.
(Ⅱ)由(1)及![]() 可知:仅当极大值等于零,即
可知:仅当极大值等于零,即![]() 时,符合要求.
时,符合要求.
此时, ![]() 就是函数
就是函数![]() 在区间
在区间![]() 的唯一零点
的唯一零点![]() .
.
所以![]() ,从而有
,从而有![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
再由(1)知: ![]() ,
, ![]() ,
, ![]() 单调递减,
单调递减,
又因为![]() ,
, ![]() ,
,
所以![]() ,即
,即![]()
点晴:本题考查函数导数与单调性.确定零点的个数问题:可利用数形结合的办法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】定义:对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f(x),则称f(x)为“局部奇函数”.
(1)已知二次函数f(x)=ax2+2x﹣4a(a∈R),试判断f(x)是否为定义域R上的“局部奇函数”?若是,求出满足f(﹣x)=﹣f(x)的x的值;若不是,请说明理由;
(2)若f(x)=2x+m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围.
(3)若f(x)=4x﹣m2x+1+m2﹣3为定义域R上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1
(1) 求数列{an}的通项公式;
(2) 设数列{bn}的前n项和Tn,且Tn+![]() = λ(λ为常数),令cn=b2n,(n∈N).求数列{cn}的前n项和Rn.
= λ(λ为常数),令cn=b2n,(n∈N).求数列{cn}的前n项和Rn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在区间(﹣1,1)上的奇函数,且f(2)=
是定义在区间(﹣1,1)上的奇函数,且f(2)= ![]() ,
,
(1)确定函数f(x)的解析式;
(2)用定义法证明f(x)在区间(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() (a∈R),且f(1)>f(3),f(2)>f(3)( )
(a∈R),且f(1)>f(3),f(2)>f(3)( )
A.若k=1,则|a﹣1|<|a﹣2|
B.若k=1,则|a﹣1|>|a﹣2|
C.若k=2,则|a﹣1|<|a﹣2|
D.若k=2,则|a﹣1|>|a﹣2|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|ax2+bx+1=0}(a∈R,b∈R),集合B={﹣1,1}.
(1)若BA,求实数a的值;
(2)若A∩B≠,求a2﹣b2+2a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合I={1,2,3,4,5},集合A,B为集合I的两个非空子集,若集合A中元素的最大值小于集合B中元素的最小值,则满足条件的A,B的不同情形有( )种.
A.46
B.47
C.48
D.49
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com