练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi（单位：千元）与月储蓄yi（单位：千元）的数据资料，算得 =80， =20， iyi=184， =720．（b= ）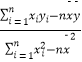
    （1）求家庭的月储蓄y对月收入x的线性回归方程；
    （2）判断变量x与y之间是正相关还是负相关；
    （3）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．

    【答案】
    （1）解：由题意知，n=10， =8， =2，

    ∴b= =0.3，a=2﹣0.3×8=﹣0.4，

    ∴y=0.3x﹣0.4．


    （2）解：由于b=0.3＞0，

    ∴y与x之间是正相关．


    （3）解：x=7时，y=0.3×7﹣0.4=1.7（千元）
    【解析】（1）由题意可知n， ， ，进而代入可得b、a值，可得方程；（2）由回归方程x的系数b的正负可判断；（3）把x=7代入回归方程求其函数值即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆C经过点，且圆心在直线上，又直线与圆C交于P,Q两点.

    （1）求圆C的方程；

    （2）若，求实数的值；

    (3)过点作直线，且交圆C于M,N两点，求四边形的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为抛物线的焦点，过的直线与交于两点， 为中点，点到轴的距离为， .

    （1）求的值；

    （2）过分别作的两条切线， .请选择轴中的一条，比较到该轴的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位附近只有甲、乙两个临时停车场，它们各有个车位，为了方便市民停车，某互联网停车公司对这两个停车场，在某些固定时刻的剩余停车位进行记录，如下表：

    时间

    停车场

    点

    点

    点

    点

    点

    点

    甲停车场

    乙停车场

    如果表中某一时刻剩余停车位数低于该停车场总车位数的，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报.

    （1）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；

    （2）从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率；

    （3）当乙停车场发出饱和警报时，求甲停车场也发出饱和警报的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高一年级学生中随机抽取40名中学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段： ， ，…， ，得到如图所示的频率分布直方图.

    （1）求图中实数的值；

    （2）若该校高一年级共有640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；

    （3）若从数学成绩在与两个分数段内的学生中随机选取2名学生，求这2名学生的数学成绩之差的绝对值不大于10的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}中，a1=2，an+1﹣an﹣2n﹣2=0（n∈N*）．
    （1）求数列{an}的通项公式；
    （2）设 ，若对任意的正整数n，当m∈[﹣1，1]时，不等式 恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示， 矩形所在的平面， 分别是的中点.

    （1）求证： 平面；

    （2）求证： .

    （3）当满足什么条件时，能使平面成立？并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|a﹣1＜x＜2a+1}，B={x|0＜x＜1}
    （1）若a= ， 求A∩B．
    （2）若A∩B=，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x∈R，符号[x]表示不超过x的最大整数，若函数f（x）=（x＞0），则给出以下四个结论：
    ①函数f（x）的值域为[0，1]；
    ②函数f（x）的图象是一条曲线；
    ③函数f（x）是（0，+∞）上的减函数；
    ④函数g（x）=f（x）﹣a有且仅有3个零点时 ．
    其中正确的序号为 ．

    查看答案和解析>>

    同步练习册答案