
【题目】已知函数![]() .
.
(1)若![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
(2)若![]() 在
在![]() 只有一个零点,求
只有一个零点,求![]() .
.
【答案】(1)见解析(2)![]()
【解析】分析:(1)先构造函数![]() ,再求导函数,根据导函数不大于零得函数单调递减,最后根据单调性证得不等式,(2)研究
,再求导函数,根据导函数不大于零得函数单调递减,最后根据单调性证得不等式,(2)研究![]() 零点,等价研究
零点,等价研究![]() 的零点,先求
的零点,先求![]() 导数:
导数:![]() ,这里产生两个讨论点,一个是a与零,一个是x与2,当
,这里产生两个讨论点,一个是a与零,一个是x与2,当![]() 时,
时,![]() ,
,![]() 没有零点;当
没有零点;当![]() 时,
时,![]() 先减后增,从而确定只有一个零点的必要条件,再利用零点存在定理确定条件的充分性,即得a的值.
先减后增,从而确定只有一个零点的必要条件,再利用零点存在定理确定条件的充分性,即得a的值.
详解:(1)当![]() 时,
时,![]() 等价于
等价于![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减.
单调递减.
而![]() ,故当
,故当![]() 时,
时,![]() ,即
,即![]() .
.
(2)设函数![]() .
.
![]() 在
在![]() 只有一个零点当且仅当
只有一个零点当且仅当![]() 在
在![]() 只有一个零点.
只有一个零点.
(i)当![]() 时,
时,![]() ,
,![]() 没有零点;
没有零点;
(ii)当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
故![]() 是
是![]() 在
在![]() 的最小值.
的最小值.
①若![]() ,即
,即![]() ,
,![]() 在
在![]() 没有零点;
没有零点;
②若![]() ,即
,即![]() ,
,![]() 在
在![]() 只有一个零点;
只有一个零点;
③若![]() ,即
,即![]() ,由于
,由于![]() ,所以
,所以![]() 在
在![]() 有一个零点,
有一个零点,
由(1)知,当![]() 时,
时,![]() ,所以
,所以![]() .
.
故![]() 在
在![]() 有一个零点,因此
有一个零点,因此![]() 在
在![]() 有两个零点.
有两个零点.
综上,![]() 在
在![]() 只有一个零点时,
只有一个零点时,![]() .
.


科目:高中数学 来源: 题型:
【题目】2019年是中华人民共和国成立70周年,某校党支部举办了一场“我和我的祖国”知识竞赛,满分100分,回收40份答卷,成绩均落在区间![]() 内,将成绩绘制成如下的频率分布直方图.
内,将成绩绘制成如下的频率分布直方图.
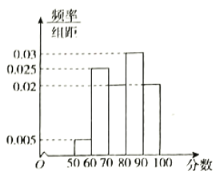
(1)估计知识竞赛成绩的中位数和平均数;
(2)从![]() ,
,![]() 分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于
分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
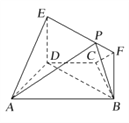
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)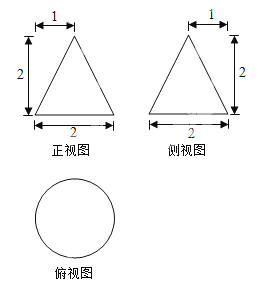
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com