
【题目】已知直线l过点A(2,4),且被平行直线l1:x-y+1=0与l2:x-y-1=0所截的线段中点M在直线x+y-3=0上,求直线l的方程.
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() .
.
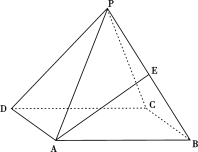
(1)求正四棱锥![]() 的外接球半径;
的外接球半径;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某篮球比赛中,根据甲和乙两人的得分情况得到如图所示的茎叶图.

(1)从茎叶图的特征来说明他们谁发挥得更稳定;
(2)用样本的数字特征验证他们谁发挥得更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥顶点为![]() ,底面圆心为
,底面圆心为![]() ,其母线与底面所成的角为45°,
,其母线与底面所成的角为45°,![]() 和
和![]() 是底面圆
是底面圆![]() 上的两条平行的弦,
上的两条平行的弦,![]() .
.

(1)证明:平面![]() 与平面
与平面![]() 的交线平行于底面;
的交线平行于底面;
(2)求轴![]() 与平面
与平面![]() 所成的角的正切值.
所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
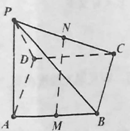
(1)求平面![]() 和平面
和平面![]() 所成二面角的大小;
所成二面角的大小;
(2)求证:![]() 平面
平面![]() ;
;
(3)当![]() 的长度变化时, 求异面直线
的长度变化时, 求异面直线![]() 与
与![]() 所成角的可能范围.
所成角的可能范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间生产一种仪器的固定成本是![]() 元,每生产一台该仪器需要增加投入
元,每生产一台该仪器需要增加投入![]() 元,已知总收入满足函数:
元,已知总收入满足函数: ,其中
,其中![]() 是仪器的月产量.
是仪器的月产量.
(利润=总收入-总成本).
(1)将利润表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,车间所获利润最大?最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
:![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
(1)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设![]() 为坐标原点,直线
为坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .证明:存在实数
.证明:存在实数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线l经过第二、三、四象限,则直线l的倾斜角的范围是 ( )
A. 0°≤α<90° B. 90°≤α<180°
C. 90°<α<180° D. 0°≤α<180°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】育才高中为了推进新课程改革,满足不同层次学生的需求,决定在每周的周一、周三、周五的课外活动期间同时开设“茶艺”、“模拟驾驶”、“机器人制作”、“数学与生活”和“生物与环境”选修课,每位有兴趣的同学可以在任何一天参加任何一门科目.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各选修课各天的满座的概率如下表:
生物与环境 | 数学与生活 | 机器人制作 | 模拟驾驶 | 茶艺 | |
周一 |
|
|
|
|
|
周三 |
|
|
|
|
|
周五 |
|
|
|
|
|
(1)求茶艺选修课在周一、周三、周五都不满座的概率;
(2)设周三各选修课中满座的科目数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com