练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某市“招手即停”公共汽车的票价按下列规则制定：5公里以内(含5公里)，票价2元；5公里以上，每增加5公里，票价增加1元(不足5公里的按5公里计算)．如果某条线路的总里程为20公里，

    （1）请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象．

    （2）与在(5，10]内有且仅有1个公共点，求a范围.

    【答案】（1）,图像见解析（2）

    【解析】

    （1）分，，，四种情况求票价与里程之间的函数解析式；（2）是单调递增函数，并且过点，根据（1）的图象可知，若在内有且仅有1个公共点，只需满足 ，求的范围.

    (1)设票价为y元，里程为x公里．由题意可知，自变量x的取值范围是(0，20]．

    由“招手即停”公共汽车票价的制定规则．可得到以下函数解析式：

    根据这个函数解析式，可画出函数图象，

    (2)由图知

    解得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设抛物线C:的焦点为F，抛物线上的点A到轴的距离等于.

    （1）求抛物线C的方程；

    （2）已知经过抛物线C的焦点F的直线与抛物线交于A，B两点，证明： 为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）若，求的取值范围；

    （Ⅱ）证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数().

    （1）若为偶函数，求的值；

    （2）若的解集为，求a,b的值;

    （3）若在区间上单调递增，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】探究函数，上的最小值，并确定取得最小值时的值，列表如下：

    …

    0.5

    1

    1.5

    1.7

    1.9

    2

    2.1

    2.2

    2.3

    3

    4

    5

    7

    …

    …

    14

    7

    5.34

    5.11

    5.01

    5

    5.01

    5.04

    5.08

    5.67

    7

    8.6

    12.14

    …

    （1）观察表中值随值变化趋势特点，请你直接写出函数，的单调区间，并指出当取何值时函数的最小值为多少；

    （2）用单调性定义证明函数在上的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若，且直线是曲线的一条切线，求实数的值；

    （2）若不等式对任意恒成立，求的取值范围；

    （3）若函数有两个极值点，，且，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，圆与圆有公共点，则实数的取值范围是___．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行，这是2017年我国重要的主场外交活动，对推动国际和地区合作具有重要意义．某高中政教处为了调查学生对“一带一路”的关注情况，在全校组织了“一带一路知多少”的知识问卷测试，并从中随机抽取了12份问卷，得到其测试成绩（百分制），如茎叶图所示．

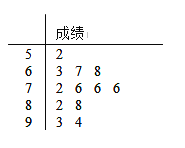
    （1）写出该样本的众数、中位数，若该校共有3000名学生，试估计该校测试成绩在70分以上的人数；

    （2）从所抽取的70分以上的学生中再随机选取4人．

    ①记表示选取4人的成绩的平均数，求；

    ②记表示测试成绩在80分以上的人数，求的分布和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x）是定义在R上的奇函数，当x＜0时，f（x）=x+1，那么不等式2f（x）﹣1＜0的解集是_________

    查看答案和解析>>

    同步练习册答案