
【题目】选修4-4 坐标系与参数方程
已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 时,
时,![]() 有极值.
有极值.
(1)求![]() 的值;
的值;
(2)求![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() (2)最小
(2)最小![]() ,最大13
,最大13
【解析】试题分析:(1)求导,![]() 则
则![]() ,
,
则根据已知切线方程可得![]() ①,
①,![]() ,②,
,②,
又若![]() 时,
时,![]() 有极值,则
有极值,则![]() (,③,
(,③,
由①②③联立方程组,;解出即得![]() ;
;
(2)利用导数求出区间![]() 内的极值与端点处函数值,然后进行大小比较,其中最大者为最大值,最小者为最小值;
内的极值与端点处函数值,然后进行大小比较,其中最大者为最大值,最小者为最小值;
试题解析:(1)f′(x)=3x2+2ax+b,
则f(﹣1)=a﹣b+c﹣1,f′(﹣1)=﹣2a+b+3,
故切线方程是:y=(3﹣2a+b)x+(﹣a+c+2),
而切线方程是:y=﹣5x+5,
故3﹣2a+b=﹣5,①,
a﹣c﹣2=﹣5,②,
若![]() 时,y=f(x)有极值,
时,y=f(x)有极值,
则f′(![]() )=
)=![]() +
+![]() +b=0,③,
+b=0,③,
由①②③联立方程组,解得:![]() ;
;
(2)由(1)f(x)=x3+2x2﹣4x+5,
f′(x)=3x2+4x﹣4=(3x﹣2)(x+2),
令f′(x)>0,解得:x>![]() 或x<﹣2,
或x<﹣2,
令f′(x)<0,解得:﹣2<x<![]() ,
,
故f(x)在[﹣3,﹣2)递增,在(﹣2,![]() )递减,在(
)递减,在(![]() ,2]递减,
,2]递减,
由f(﹣3)=8,f(﹣2)=13,f(![]() )=
)=![]() ,f(2)=13,
,f(2)=13,
故函数的最小值是f(![]() )=
)=![]() ,
,
最大值是f(2)=f(﹣2)=13.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】利用随机数表法对一个容量为500编号为000,001,002,…,499的产品进行抽样检验,抽取一个容量为10的样本,若选定从第12行第5列的数开始向右读数,(下面摘取了随机数表中的第11行至第15行),根据下图,读出的第3个数是( ) 
A.841
B.114
C.014
D.146
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD﹣A1B1C1D1为正方体,下面结论错误的是( ) 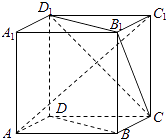
A.BD∥平面CB1D1
B.AC1⊥BD
C.异面直线AD与CB1角为60°
D.AC1⊥平面CB1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2016年粮食产量的部分数据如下表:

(1)求该地区2008年至2016年的粮食年产量![]() 与年份
与年份![]() 之间的线性回归方程;
之间的线性回归方程;
(2)利用(1)中的回归方程,分析2008年至2016年该地区粮食产量的变化情况,并预测该地区 2018年的粮食产量.
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,建立空间直角坐标系Dxyz,已知正方体ABCD﹣A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,点N在棱CC1上. 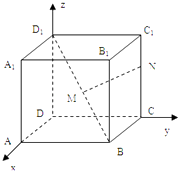
(1)当2|C1N|=|NC|时,求|MN|;
(2)当点N在棱CC1上移动时,求|MN|的最小值并求此时的N点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,M、N分别是棱AA1、AD的中点,设E是棱AB的中点. 
(1)求证:MN∥平面CEC1;
(2)求平面D1EC1与平面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若aα,bβ,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com