
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)对任意的![]() ,
, ![]() ,恒有
,恒有![]() ,求正实数
,求正实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)先确定函数的定义域然后求导数fˊ(x),再对字母a分类讨论,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间.
(2)根据第一问的单调性,知f(x)在[1,2]上为减函数.若x1=x2,则原不等式恒成立;若x1≠x2,不妨设1≤x1<x2≤2,则f(x1)>f(x2),![]() ,所以原不等式进行化简整理得
,所以原不等式进行化简整理得![]() 对任意的
对任意的![]() 恒成立,令
恒成立,令![]() ,转化成研究g(x)在[1,2]的单调性,再利用导数即可求出正实数λ的取值范围.
,转化成研究g(x)在[1,2]的单调性,再利用导数即可求出正实数λ的取值范围.
试题解析:
(1)![]() =
=![]() ,
,
令f'(x)=0,则x1=2a+1,x2=1.
①当a=0时,![]() ,所以f(x)增区间是(0,+∞);
,所以f(x)增区间是(0,+∞);
②当a>0时,2a+1>1,
所以f(x)增区间是(0,1)与(2a+1,+∞),减区间是(1,2a+1);
③当![]() 时,0<2a+1<1,
时,0<2a+1<1,
所以f(x)增区间是(0,2a+1)与(1,+∞),减区间是(2a+1,1);
④当![]() 时,2a+1≤0,
时,2a+1≤0,
所以f(x)增区间是(1,+∞),减区间是(0,1).
(2)因为![]() ,所以(2a+1)∈[4,6],
,所以(2a+1)∈[4,6],
由(1)知f(x)在[1,2]上为减函数.
若x1=x2,则原不等式恒成立,∴λ∈(0,+∞).
若x1≠x2,不妨设1≤x1<x2≤2,则f(x1)>f(x2),![]() ,
,
所以原不等式即为:![]() ,
,
即![]() 对任意的
对任意的![]() ,x1,x2∈[1,2]恒成立.
,x1,x2∈[1,2]恒成立.
令![]() ,
,
所以对任意的![]() ,x1,x2∈[1,2]有g(x1)<g(x2)恒成立,
,x1,x2∈[1,2]有g(x1)<g(x2)恒成立,
所以![]() 在闭区间[1,2]上为增函数.
在闭区间[1,2]上为增函数.
所以g'(x)≥0对任意的![]() ,x∈[1,2]恒成立.
,x∈[1,2]恒成立.
而![]() ,g'(x)=x﹣(2a+2)
,g'(x)=x﹣(2a+2)![]() ,化简即x3﹣(2a+2)x2+(2a+1)x+λ≥0,
,化简即x3﹣(2a+2)x2+(2a+1)x+λ≥0,
即(2x﹣2x2)a+x3﹣2x2+x+λ≥0,其中![]() .
.
∵x∈[1,2],∴2x﹣2x2≤0,∴只需![]() .
.
即x3﹣7x2+6x+λ≥0对任意x∈[1,2]恒成立.
令h(x)=x3﹣7x2+6x+λ,x∈[1,2],h'(x)=3x2﹣14x+6<0恒成立.
∴h(x)=x3﹣7x2+6x+λ在闭区间[1,2]上为减函数,则hmin(x)=h(2)=λ﹣8,
∴hmin(x)=h(2)=λ﹣8≥0,解得λ≥8.
故正实数λ的取值范围[8,+∞)


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线方程为x2=2py(p>0),其焦点为F,点O为坐标原点,过焦点F作斜率为k(k≠0)的直线与抛物线交于A,B两点,过A,B两点分别作抛物线的两条切线,设两条切线交于点M.
(1)求 ![]() ;
;
(2)设直线MF与抛物线交于C,D两点,且四边形ACBD的面积为 ![]() ,求直线AB的斜率k.
,求直线AB的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是 ![]() .
.
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ.求ξ的分布列及数学期望E(ξ).( 结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设 ![]() =m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( )
=m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点,F为AC和BD的交点.
(1)证明:PB∥平面AEC;
(2)证明:平面PAC⊥平面PBD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知等边![]() 中,
中,![]() 分别为
分别为![]() 边的中点,
边的中点,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,使平面
的位置,使平面![]() 平面EFCB.
平面EFCB.
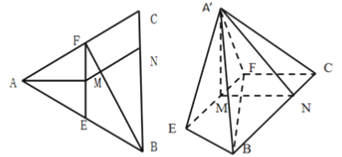
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com