
【题目】已知圆C:(x+2)2+y2=1,P(x,y)为圆C上任一点,
(1)求 ![]() 的最大、最小值;
的最大、最小值;
(2)求x﹣2y的最大、最小值.
【答案】
(1)解:设k= ![]() ,则y﹣2=kx﹣k,即直线方程为kx﹣y+2﹣k=0,
,则y﹣2=kx﹣k,即直线方程为kx﹣y+2﹣k=0,
∵P(x,y)为圆C上任一点,
∴则圆心(﹣2,0)到直线的距离d= ![]() =
= ![]() ≤1,
≤1,
即|2﹣3k| ![]() ,
,
平方得8k2﹣12k+3≤0,
解得 ![]() ≤k≤
≤k≤ ![]() ,
,
故 ![]() 的最大值为
的最大值为 ![]() ,最小值为
,最小值为 ![]()
(2)解:设b=x﹣2y,j即x﹣2y﹣b=0,
∵P(x,y)为圆C上任一点,
∴则圆心(﹣2,0)到直线的距离d= ![]() ,
,
即|b+2|≤ ![]() ,
,
则﹣2﹣ ![]() ≤b≤
≤b≤ ![]() ﹣2,
﹣2,
即x﹣2y的最大值为 ![]() ﹣2,最小值为﹣2﹣
﹣2,最小值为﹣2﹣ ![]()
【解析】(1)设k= ![]() ,利用直线和圆的位置关系即可得到结论;(2)设z=x﹣2y,利用直线和圆的位置关系即可得到结论.
,利用直线和圆的位置关系即可得到结论;(2)设z=x﹣2y,利用直线和圆的位置关系即可得到结论.
【考点精析】通过灵活运用圆的标准方程,掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程即可以解答此题.
;圆心为A(a,b),半径为r的圆的方程即可以解答此题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】为了迎接珠海作为全国文明城市的复查,爱卫会随机抽取了60位路人进行问卷调查,调查项目是自己对珠海各方面卫生情况的满意度(假设被问卷的路人回答是客观的),以分数表示问卷结果,并统计他们的问卷分数,把其中不低于50分的分成五段[50,60),[60,70),…[90,100]后画出如图部分频率分布直方图,观察图形信息,回答下列问题: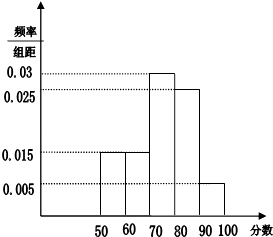
(1)求出问卷调查分数低于50分的被问卷人数;
(2)估计全市市民满意度在60分及以上的百分比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为备战![]() 年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得
年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得![]() 分,负者得
分,负者得![]() 分,在每一场比赛中,甲胜乙的概率为
分,在每一场比赛中,甲胜乙的概率为![]() ,丙胜甲的概率为
,丙胜甲的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为
,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设在该次对抗比赛中,丙得分为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 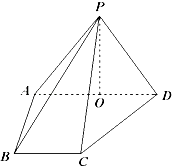
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com